Propiedad conmutativa del producto o multiplicación
\( a\cdot b = b\cdot a\)
"El orden de los factores no altera el producto."
En esta página explicamos qué es la propiedad conmutativa del producto (o multiplicación) de números reales y proporcionamos algunos ejemplos. También, resolvemos algunos problemas resueltos.
Índice:
- Producto de naturales como suma
- Propiedad conmutativa del producto
- Otros ejemplos
- Problemas resueltos
- Otras operaciones
1. Producto de naturales como suma
Normalmente, aprendemos a multiplicar a partir de las tablas de multiplicación, pero la multiplicación (o producto) de números naturales puede verse como una forma abreviada de calcular sumas.
El producto de los números naturales \(a\) y \(b\) se escribe como \(a\times b\) o como \(a \cdot b\) y es el resultado de sumar \(a\) veces el número \(b\) consigo mismo:
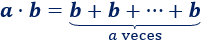
Ejemplos
- El producto \(2\cdot 3\) se calcula sumando \(2\) veces el número \(3\):
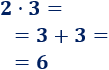
- El producto \(3\cdot 5\) se calcula sumando \(3\) veces el número \(5\):
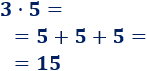
2. Propiedad conmutativa del producto
El producto de números es una operación conmutativa, lo que quiere decir que el producto \(a\cdot b\) tiene el mismo resultado que el producto \(b\cdot a\):
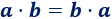
Solemos referirnos a esta propiedad con la siguiente frase:
El orden de los factores no altera el producto.
Y es que, en efecto, tenemos el mismo resultado sumando \(a\) veces el número \(b\) que sumando \(b\) veces el número \(a\).
Ejemplo
- Calculamos el producto \(2\cdot 4\):
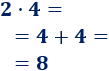
- Calculamos el producto \(4\cdot 2\):

Ambas operaciones tienen el mismo resultado.
3. Otros ejemplos
La propiedad conmutativa del producto de números (reales) siempre se cumple. Ahora vamos a mostrar algunos ejemplos más complejos.
Producto con signos (números enteros)
Consideremos la multiplicación de \(-2\) y \(3\):

Si aplicamos la propiedad conmutativa, tenemos
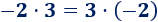
Nota: Recordad que el número de detrás del punto de multiplicación debe estar entre paréntesis si tiene signo.
Enlace: operaciones con números enteros.
Producto con suma
Consideremos la multiplicación del número \(2\) y de la suma \(1+2\):
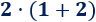
Aplicando la propiedad conmutativa,
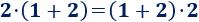
El resultado de ambas operaciones (que son iguales) es \(6\).
Nota: la suma se escribe entre paréntesis porque la multiplicación afecta a los dos sumandos.
Enlace: Número por un paréntesis.
Producto con raíces
Las raíces también son números, así que su producto también cumple la propiedad conmutativa, por ejemplo,
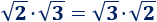
Enlace: Producto de raíces.
Producto con parámetros o incógnitas
Las letras suelen representar números, así que su producto también conmuta:
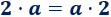
De hecho, siempre se aconseja escribir las letras detrás del número, haciendo uso de la propiedad conmutativa.
Importante:
La propiedad conmutativa de la multipliación se cumple siempre, independientemente del número de factores que haya en la multiplicación. Por ejemplo,
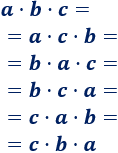
Todas las multiplicaciones escritas tienen el mismo resultado, independientemente de la posición que ocupe cada factor.
4. Problemas resueltos
Problema 1
Comprobar, mediante la propiedad conmutativa, que
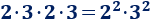
Solución:
El cuadrado de \(2\) y de \(3\) es
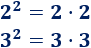
Reordenando los \(4\) factores de la multiplicación mediante la propiedad conmutativa, tenemos:

Problema 2
¿Es cierta la siguiente igualdad?
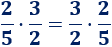
Solución:
Aunque haya fracciones (que son divisiones), la operación principal es un producto, y el producto es conmutativo.
Un forma de comprobar la conmutatividad del producto de fracciones es ver las fracciones como números:
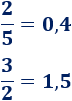
De este modo, podemos escribir el producto de las fracciones como un producto de números y aplicar la propiedad conmutativa del producto:
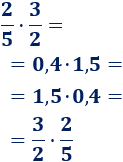
Por tanto, la igualdad del problema es cierta, aunque esto no significa en absoluto que la división sea conmutativa, porque no lo es. Se trata de la conmutatividad del producto.
Problema 3
¿Es cierta la siguiente igualdad?
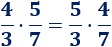
Solución:
Recordad la multiplicación de dos fracciones:
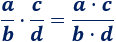
Por tanto,
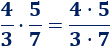
Ahora, como el producto de números es conmutativo, podemos cambiar el orden de los factores del numerador:
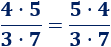
Y sabemos, por lo dicho anteriormente,
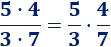
En resumen, tenemos
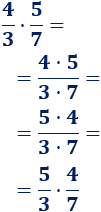
Por tanto, la igualdad del problema es cierta.
5. Otras operaciones
Esta página está dedicada al producto o multiplicación, pero esta no es la única operación matemática que cumple la propiedad conmutativa.
La suma de números (y fracciones) es conmutativa.
Ejemplo
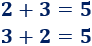
La resta de números (y fracciones) no es conmutativa.
La resta, considerada como una operación entre dos números naturales, no es una operación conmutativa.
Ejemplo
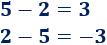
La potenciación no es conmutativa.
Ejemplo
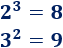
La división no es conmutativa.
Por lo general, \(a\) dividido entre \(b\) no es igual a \(b\) dividido entre \(a\).
Ejemplo
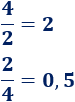
La unión de conjuntos es conmutativa.
Ejemplo
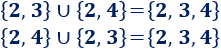
La intersección de conjuntos es conmutativa.
Ejemplo
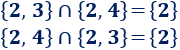
Otras operaciones más avanzadas:
- La suma y el producto escalar de vectores son operaciones conmutativas.
- La suma y el producto de números complejos son operaciones conmutativas.
- La suma de matrices cuadradas reales es conmutativa, pero su producto no lo es.
Otros temas relacionados:
- Número por paréntesis
- Paréntesis por paréntesis
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899