Producto y cuadrado de raíces cuadradas
En esta página explicamos la propiedad del producto de raíces cuadradas, la del cuadrado de una raíz cuadrada y la de la raíz cuadrada de un cuadrado. Estas sencillas propiedades son útiles tanto a la hora de calcular raíces como a la hora de simplificar expresiones algebraicas con raíces.
Índice:
- Producto de raíces
- Raíz de un cuadrado
- Cuadrado de una raíz
- Problemas resueltos
1. Producto de raíces
La raíz cuadrada de un producto de factores es igual al producto de las raíces cuadradas de los factores:
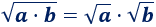
Por ejemplo, la raíz cuadrada de 2 por la de 3 es la raíz cuadrada de 6:
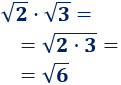
2. Raíz de un cuadrado
Recordad que la raíz cuadrada de \(a\) es el número \(b\) tal que \(b^2 = a\):

Por ejemplo, como 2 al cuadrado es 4, la raíz cuadrada de 4 es 2:
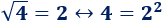
Teniendo en cuanta esto, la raíz cuadrada de \(a^2\) es \(a\) (porque \(a\) al cuadrado es \(a^2\)):
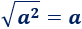
Podemos demostrarlo usando la definición anterior:
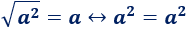
Ejemplos:
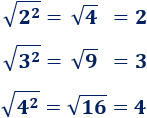
3. Cuadrado de una raíz
El cuadrado de la raíz cuadrada de \(a\) es \(a\):
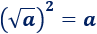
Esta propiedad es consecuencia de la anterior, se obtiene al escribir el cuadrado como un producto:
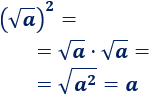
Observad que podemos introducir o extraer el cuadrado de la raíz:
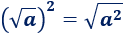
Ejemplos:
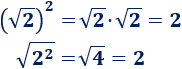
4. Problemas resueltos
Problema 1
Calcular los siguientes productos de raíces:
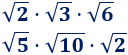
Solución:
Primer producto:
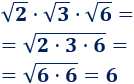
Segundo producto:
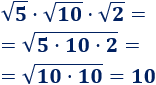
Problema 2
Calcular los siguientes productos de raíces:
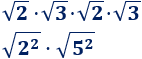
Solución:
Primer producto:
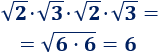
Segundo producto:
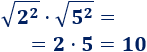
Problema 3
Calcular la raíz cuadrada de 256 como la raíz de un producto.
Solución:
Descomponemos el número 256:
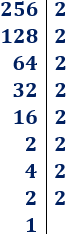
Por tanto, podemos escribir 256 como una potencia de 2:
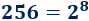
Teniendo en cuenta las propiedades de las potencias (en un producto de potencias con la misma base podemos sumar los exponentes):
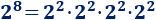
Ahora, aplicamos la propiedad de la raíz cuadrada del producto:
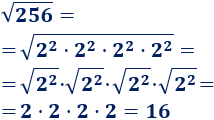
Problema 4
¿Cuál es el resultado de la siguiente operación?
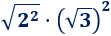
Solución:
Recordad que el cuadrado puede entrar y salir de la raíz cuadrada:
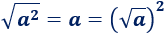
Por tanto,
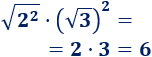
Problema 5
Comprobar si es cierto que la raíz cuadrada de una suma es igual a la suma de las raíces cuadradas, es decir,
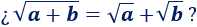
Solución:
Calculamos la raíz cuadrada de 2+2:
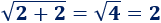
Y la suma de dos raíces cuadradas de 2:
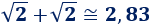
Por tanto, la igualdad no es cierta.
Más información en desigualdad tringular y raíz de la suma.