Desigualdad triangular
$$ |x+y| \leq |x|+|y|$$
En esta página demostramos la desigualdad triangular o de Minkowski para valores de \(\mathbb{R}\), es decir, que el valor absoluto de la suma es menor o igual que la suma de los valores absolutos. Para poder demostrarlo, veremos primero algunas propiedades que necesitamos. Aprovechando la ocasión, demostramos también que la raíz de una suma es menor o igual que la suma de sus raíces, es decir,
$$\sqrt{x+y}\leq \sqrt{x} + \sqrt{y}$$
Índice:
- Ejemplo
- Valor absoluto menor que un número
- Propiedad del valor absoluto
- Demostración de \(|x+y| ≤ |x|+|y|\)
- Desigualdad triangular para raíces: \(\sqrt{x+y}\leq \sqrt{x} + \sqrt{y}\) para \(x,y\geq 0\)
1. Ejemplo
Veamos un ejemplo de la desigualdad triangular:
Sean \(x = 2\) e \(y = -3\).
El valor absoluto de su suma es
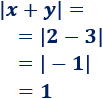
La suma de sus valores absolutos es
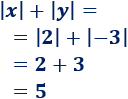
Como \(1 ≤ 5\), se verifica la desigualdad:

2. Valor absoluto menor que un número
Nos interesa la siguiente propiedad del valor absoluto:
\(|a|≤ b\) si y sólo si \(-b ≤ a ≤ b\)
Es decir,
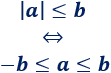
Ejemplo:
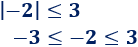
3. Propiedad del valor absoluto
Finalmente, necesitamos otra propiedad del valor absoluto:
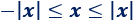
Esta propiedad es evidente, pero la usaremos más adelante.
Ejemplos:
- Si \(x=2\),
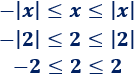
- Si \(x=-2\),
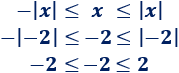
4. Demostración
Para todo par \(x\) e \(y\),
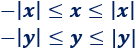
Sumando las desigualdades,
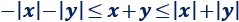
Es decir,
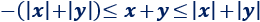
Ahora, aplicamos la propiedad vista en el segundo aparatado (si \(-b ≤ a ≤ b\) entonces \(|a|≤ b\)) y tenemos

5. Desigualdad triangular para raíces
\(\sqrt{x+y}\leq \sqrt{x} + \sqrt{y}\) para \(x,y\geq 0\)
Obviamente, \(x,y ≥ 0\) para poder escribir sus raíces cuadradas.
Ejemplo:
Sean \(x = 1\) e \(y = 2\).
La raíz de la suma es
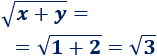
La suma de las raíces es
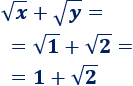
Se cumple la desigualdad:

Para demostrar esta desigualdad, calculamos el cuadrado de la suma de las raíces:
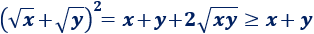
Por tanto, tenemos
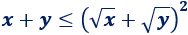
Ahora, tomando raíces cuadradas*, tenemos

*Demostramos a continuación que
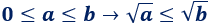
Supongamos que la implicación no es cierta, por tanto,

Multiplicando por \(\sqrt{a}\) y usando que \(\sqrt{a}> \sqrt{b}\) tenemos
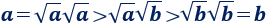
Luego tenemos que \(a > b\), lo cual contradice la hipótesis inicial.