Números pares e impares
En esta página definimos los números pares y los impares y enunciamos y demostramos algunas propiedades básicas, como que la suma de números pares es par. También, definimos número natural, entero, divisible y múltiplo para ayudarnos en los razonamientos. Con ejemplos y problemas resueltos.
Índice:
- Natural y entero
- Número múltiplo y divisible
- Número par
- Número impar
- Algunas propiedades
- Problemas resueltos
- Demostraciones de las propiedades
1. Natural y entero
Los números naturales (\(\mathbb{N}\)) son los que usamos para contar: 1, 2, 3, 4…
Los números enteros (\(\mathbb{Z}\)) son el 0 y los números naturales con signo positivo y con signo negativo: 0, 1, -1, 2, -2, 3, -3…
Nota: el 0 también puede considerarse un número natural.
2. Número múltiplo y divisible
Múltiplo
Los números múltiplos del número entero \(a\) son los que se obtienen al multiplicar \(a\) por un número entero.
Ejemplo
Calculamos algunos múltiplos de 2:
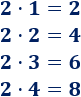
Divisible
Dados dos números enteros \(a\) y \(d\), decimos que \(d\) divide a \(a\), o bien, que \(a\) es divisible entre \(d\), si existe un número entero \(n\) tal que \( a = d\cdot c\).
Suele escribirse \(d | a\) ("\(d\) divide a \(a\)"):
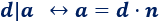
Ejemplos
- El número 6 es divisible entre 2 porque

- El número 6 es divisible entre 3 porque

- El número 15 es divisible entre 5 y entre 3:
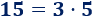
También, un número \(a\) es divisible entre \(b\) si la división \(a\) dividido entre \(d\) es un número entero y tiene resto 0.
Ejemplos
- El número 8 es divisible entre 2:
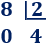
- El número 10 es divisible entre 5:
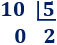
Propiedad importante:
El número \(d\) divide a \(a\) si y sólo si \(a\) es un múltiplo de \(d\).
3. Número par
Las dos siguientes definiciones son válidas:
- Los números pares son los números divisibles entre 2.
- Los números pares son los múltiplos de 2.
Por tanto, los números pares son 0, 2, -2, 4, -2, 6, -6, …
Propiedad importante:
Si la última cifra de un número es par, entonces es par.
Ejemplo
Los siguientes números son pares porque terminan en un número par: 123456, 65432, 1590, 1233217410.
Como los números pares son los múltiplos de 2, podemos decir lo siguiente:
Si \(a\) es un número par, entonces existe un número entero \(n\) tal que \(a = 2\cdot n\).
Observad que el número 0 es par porque es múltiplo de 2:

4. Número impar
Un número es impar si no es par.
Los números impares no son múltiplos ni divisibles entre un número en concreto.
Un número \(a\) es impar si existe un entero \(n\) tal que

Ejemplos
- Calculamos algunos números impares dando valores a \(n\):
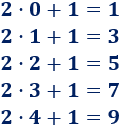
- Los siguientes números son impares por no terminar en número par: 12345, 1597, 17931 y 197460087.
5. Algunas propiedades
A continuación, enunciamos algunas propiedades de los números pares/impares. Las demostraciones se encuentran al final de la página.
La suma de números pares es par.
Por ejemplo, 2 + 8 = 10.
La suma de DOS números impares es par.
Por ejemplo, 5 + 7 = 12.
Nota: es importante aclarar que la suma de una cantidad par de impares es par y la suma de una cantidad impar de impares es impar.
La suma de un par y un impar es impar.
Por ejemplo, 4 + 5 = 9.
Ningún número impar es divisible entre 2.
Por ejemplo, la división del número impar 3 entre 2 es 1,5, que no es un número entero.
Un número es par si y solomente si su cuadrado es par: \(a\) es par \(\Leftrightarrow\) \(a^2\) es par.
Por ejemplo, como 124 es par, su cuadrado es par: 1242 = 15376.
La demostración de esta última propiedad se encuentra en un número es par si y solo si su cuadrado es par.
6. Problemas resueltos
Problema 1
Relacionar las letras latinas con las griegas para obtener oraciones verdaderas:
- a. La suma de dos pares.
- b. La suma de dos impares.
- c. La suma de 5 impares.
- d. La suma de 9 impares.
- e. La suma de múltiplos de 2.
- α. Es par.
- β. Es impar.
Solución:
a, b y e con α.
c y d con β.
Problema 2
El número 84 es par porque \( 84 = 2\cdot n\). Calcular \(n\).
Solución:
Podemos calcular \(n\) dividiendo:
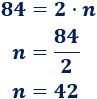
Problema 3
El número 123 es impar porque no es par. Como es impar, se puede escribir como \(123 = 2·n+1\). Calcular \(n\).
Solución:
Resolvemos como en una ecuación (pasando el 1 restando al otro lado y dividiendo entre 2):
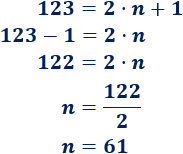
Problema 4
¿La suma de los números 12345 y 78923 es par o impar?
Solución:
Es par.
Justificación: Ambos números son impares porque NO terminan en un número par. La suma de dos impares es un número par.
Problema 5
¿La suma de los números 101010 y 928987 es par o impar?
Solución:
Es impar.
Justificación: El número 101010 es par porque termina en 0, que es par; y el número 928987 es impar porque termina en impar. La suma de un par y un impar es impar.
7. Demostración de las propiedades
La suma de números pares es par.
Demostración:
Sean \(a\) y \(b\) dos números pares. Pueden escribirse como
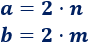
siendo \(n\) y \(m\) números enteros.
Calculamos la suma:
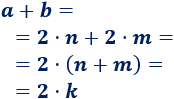
Por tanto, la suma \(a+b\) es un múltiplo de 2, puesto que se puede escribir como \(2\cdot k\) siendo \(k\) un número entero. Luego \(a+b\) es par.
La suma de dos números impares es par.
Demostración:
Dados dos números impares \(a\) y \(b\), existen dos enteros \(n\) y \(m\) tales que
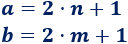
Calculamos la suma:
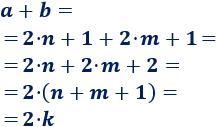
El número \(k=n+m+1\) es un entero. Como \(a+b\) se puede escribir como \(2\cdot k\), es un número par.
La suma de un par y un impar es impar.
Demostración:
Sean \(a\) par y \(b\) impar, existen dos enteros \(n\) y \(m\) tales que
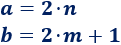
Calculamos la suma:
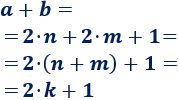
El número \(k=n+m\) es un entero. Como \(a+b\) se puede escribir como \(2\cdot k +1 \), es un número impar.
Ningún número impar es divisible entre 2.
Demostración:
Tenemos en cuenta que
- Si un número es impar, lo es porque no es par.
- Si un número es divisible entre 2, es par.
Un impar no puede ser divisible entre 2 porque si lo fuera, sería par y no puede serlo por ser impar.
Temas relacionados:
- Un número es par si y solo si su cuadrado es par
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899