Un número es par si y solo si su cuadrado es par:
$$ a^2\text{ es par} \Leftrightarrow a\text{ es par} $$
En esta página demostramos que el cuadrado de un número es par si y solo si dicho número es par. Esta propiedad, además de ser interesante por sí misma, es clave para la demostración de la irracionalidad de \(\sqrt{2}\).
También, demostramos, como consecuencia, que \(a^2\) es impar si y solo si \(a\) es par (Problema 5); y demostramos que el producto de dos números es un número par si y solo si alguno de los números es par (Problema 6).
Índice:
- Par, impar y cuadrado
- Técnicas de demostración necesarias
- Demostración de "si \(a\) es par, entonces \(a^2\) es par".
- Demostración de "si \(a^2\) es par, entonces \(a\) es par".
- Algunos ejemplos
- Problemas resueltos
1. Par, impar y cuadrado
A continuación, recordamos los conceptos y propiedades implicados en la demostración.
Número par
Por definición, un número entero \(a\) es par si existe un número entero \(n\) tal que

Otra definición, o consecuencia de la anterior, es que un número es par si es divisible entre 2.
Ejemplo
Los números 0, 2, -2, 4 y -4 son pares ya que
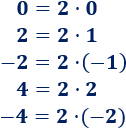
Número impar
Por definición, un número \(a\) es impar si no es un número par. Los números impares se pueden escribir como sigue, siendo \(n\) algún entero:
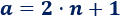
Ejemplo
Los números 1, -1, 3 y -3 son impares:
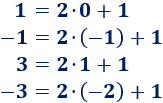
Potencia al cuadrado
Sea \(a\) un número, se define su cuadrado (potencia "elevado a 2") como el producto de \(a\) por sí mismo:
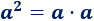
Ejemplo
El cuadrado de 0, de 2 y de -3 es 0, 4 y 9, respectivamente:
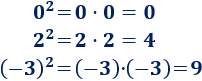
Veamos algunas propiedades de los cuadrados:
Cuadrado de un producto
El cuadrado de un producto es el cuadrado de los factores del producto:
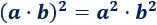
Ejemplo
Calculamos el cuadrado de \(2\cdot 3\):
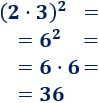
Calculamos el producto de los cuadrados:
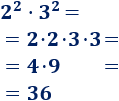
Cuadrado de la suma
El cuadrado de una suma es
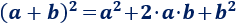
Ejemplo
Calculamos el cuadrado de 1 + 2:
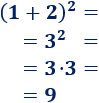
Calculamos el cuadrado aplicando la fórmula:
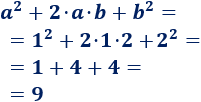
Finalmente, el producto de números enteros es un entero, lo que implica que el cuadrado de un entero también es un entero.
2. Técnicas de demostración necesarias
En esta página queremos demostrar las dos siguientes implicaciones:
- Si \(a\) es par, entonces \(a^2\) es par.
- Si \(a^2\) es par, entonces \(a\) es par.
Estos dos resultados tienen la forma de una implicación lógica: si A, entonces B.
Técnica 1
Una forma de demostrar la implicación "si A, entonces B" es suponer A y deducir u obtener B.
Técnica 2: reducción al absurdo
Otra forma de demostrar esta implicación es la siguiente:
- Suponer que A es cierto.
- Suponer que B es falso.
- Deducir u obtener una igualdad o propiedad que es falsa, como "A es falso" o "B es cierto".
- La deducción es que "si A, entonces B".
La lógica nos indica que, si se obtiene una falsedad (absurdo o contradicción) al realizar una suposición, dicha suposición es falsa. Este procedimiento para realizar demostraciones se denomina reducción al absurdo (reductio ad absurdum).
3. Demostración de "si \(a\) es par, entonces \(a^2\) es par".
Demostramos esta propiedad según el primer método descrito anteriormente (suponer A y deducir B).
Sea \(a\) un número par.
Como \(a\) es par, existe un entero \(n\) tal que \(a = 2\cdot n\).
Calculamos el cuadrado de \(a\) (aplicando la propiedad del cuadrado de un producto):
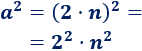
Podemos reescribir \(a^2\) como un número par:
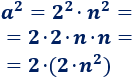
El número \(k = 2\cdot n^2\) es un número entero por ser el producto de dos enteros, por tanto, \(a^2 = 2\cdot k\) es un número par por definición.
4. Demostración de "si \(a^2\) es par, entonces \(a\) es par".
Demostramos esta propiedad por reducción al absurdo (suponer A y suponer que B es falso).
Sea \(a^2\) un número par.
Supongamos que \(a\) no es par, lo que implica que \(a\) es un número impar y, por tanto, puede escribirse como sigue, para algún entero \(n\):

Calculamos el cuadrado de \(a\) usando la fórmula para el cuadrado de la suma y el cuadrado del producto:
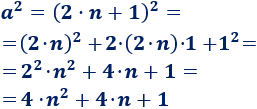
Por la propiedad distributiva,
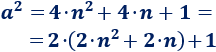
El número \(k = 2\cdot n^2 + 2\cdot n\) es un número entero, ya que
- La suma de enteros es un entero.
- El producto de enteros es un entero.
- El cuadrado de enteros es un entero.
Por tanto, \(a^2\) es un número impar, pues se puede escribir como un número impar:

Recapitulando, tenemos que \(a^2\) es impar (habiendo supuesto que \(a\) no es par), pero \(a^2\) es par por hipótesis inicial. Luego, por reducción al absurdo, \(a\) debe ser par.
5. Algunos ejemplos
- El número 6 es par y su cuadrado, 36, es par.
- El cuadrado 64 es par, así que sus raíces cuadradas, \(\sqrt{64} =\pm 8\), son números pares.
- El cuadrado de la suma de números pares es par, ya que la suma de pares es par. Por ejemplo,
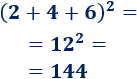
- El cuadrado de la suma de dos números impares es par, ya que la suma de dos impares es par. Por ejemplo,
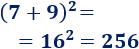
6. Problemas resueltos
Problema 1
Encontrar el número entero n para escribir los siguientes números como 2·n ó 2·n +1: 15, -9, 11 y -14.
Solución:
Escribimos el número impar 15 usando \(n = 7\):

Escribimos el número impar -9 usando \(n = -5\):
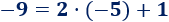
Escribimos el número impar 11 usando \(n = 5\):

Escribimos el número par -14 usando \(n = -7\):
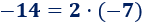
Problema 2
Determinar cuáles de los siguientes números tienen cuadrado par sin necesidad de calcularlo: 820, 123, 49780 y 101783.
Solución:
Recordad que para que un número sea par, su última cifra debe ser un número par. Por tanto, los números pares son 820 y 49780 y, por consiguiente, sus cuadrados son pares.
El cuadrado de un número impar no puede ser par, así que los restantes números no tienen cuadrado par.
Problema 3
Determinar cuáles de los siguientes cuadrados tienen raíces cuadradas pares sin necesidad de calcularlas: 441, 676, 15129 y 1522756.
Solución:
Los números 676 y 1522756 son cuadrados pares, así que sus raíces cuadradas son pares:
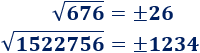
Las raíces cuadradas de los cuadrados impares 441 y 15129 son impares:
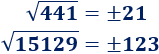
Problema 4
Determinar si los resultados de las siguientes operaciones son pares o impares:
- 2 + 4 + 6 + 8 + 10
- (2 + 8 + 20)2
- 3 + 7
- (5 + 11)2
Solución:
a. La suma de pares es un número par:
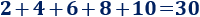
b. El cuadrado de un par es par:
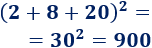
c. La suma de dos impares es par:

d. El cuadrado de un par es par:
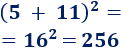
Problema 5
Demostrar que el número \(a^2\) es impar si y solo si \(a\) es impar.
Solución:
En realidad, esta propiedad es consecuencia inmediata de la propiedad "\(a^2\) es par si y solo si \(a\) es par". No obstante, podemos demostrarlo por reducción al absurdo.
Supongamos que \(a\) es impar y que \(a^2\) es par.
Como \(a^2\) es par, entonces \(a\) es par, lo cual contradice la hipótesis de que \(a\) es impar.
Obtenemos también una contradicción si suponemos que \(a\) es par y que \(a^2\) es impar.
Problema 6
Demostrar que el producto de dos números \(a\) y \(b\) es par si y solo si \(a\) es par o \(b\) es par.
Solución:
Supongamos que \(a\) es par (no importa si \(b\) es par o impar). Entonces, existe un entero \(n\) tal que \(a = 2\cdot n\).
El producto \(a\cdot b\) es
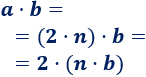
Por tanto, \(a\cdot b\) es par.
Supongamos ahora que \(a\cdot b\) es par.
Supongamos que \(a\) y \(b\) son impares. Entonces, existen dos enteros \(m\) y \(k\) tales que
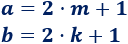
Calculamos su producto:
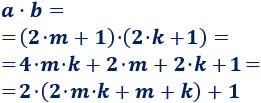
El número \(t = 2mk + m +k\) es un entero, así que \(a\cdot b\) es un número impar por tener la forma \(2\cdot t + 1\). Pero como hemos supuesto que \(a\cdot b\) es par, entonces \(a\) y \(b\) no pueden ser ambos impares, por lo que \(a\) es par o \(b\) es par.
Temas relacionados:
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899