Límites de raíces
Explicamos cómo calcular límites de funciones con raíces, especialmente, restas de raíces y cocientes de raíces de distinto orden. Con ejemplos, gráficas y problemas resueltos.
Índice:
- Límites de una raíz
- Comparación de raíces
- Límites de cocientes de raíces
- Límites de restas de raíces
1. Límites de una raíz
Veamos un par de ejemplos: el límite de la raíz cuadrada y de la raíz cúbica de \(x\) cuando \(x\) tiende a infinito.
Consideremos la función raíz cuadrada:
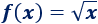
Se trata de una función que siempre crece, así que su límite es infinito cuando \(x\) tiende a infinito positivo:
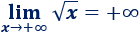
La función no está definida cuando \(x\) es negativo (no existe la raíz cuadrada de un número negativo), así que no existe el límite cuando \(x\to -\infty\).
Gráfica:
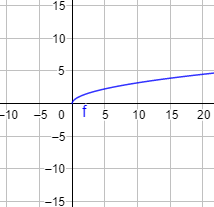
Consideremos ahora la función raíz cúbica:
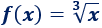
La raíz cúbica de \(x\) crece cuando \(x\) crece y decrece cuando \(x\) decrece, así que sus límites son
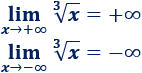
Gráfica:
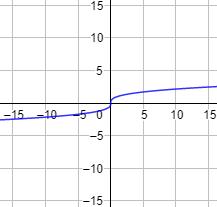
Nota: a diferencia de otras funciones, como las polinómicas o las exponenciales, las raíces crecen (o decrecen) lentamente, de ahí que al observar su gráfica no se aprecie tan claramente que su límite es infinito.
Problema 1
Calcular los siguientes límites de raíces:
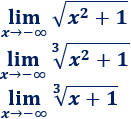
Solución:
Primer límite
El radicando nunca es negativo (porque hay un cuadrado más un número positivo), así que no importa que \(x\) tienda a infinito negativo:
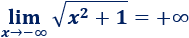
Segundo límite
El radicando es positivo, así que el límite es infinito positivo:
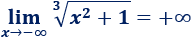
Tercer límite
El radicando es negativo cuando \(x\) toma valores menores que \(-1\), pero no supone ningún problema puesto que la raíz es cúbica:
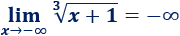
2. Comparación de raíces
La técnica que describimos a continuación nos permite simplificar los límites omitiendo sumandos de los radicandos.
Supongamos que tenemos las siguientes funciones que son raíces cuadradas de polinomios de tercer grado:
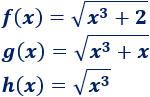
Los límites dependen de los monomios de grado mayor (en nuestro caso, es el monomio \(x^3\)). Esto de sebe a que estos monomios son los que más peso tienen en la suma cuando \(x\) toma valores muy grandes (o muy pequeños).
Como las tres funciones tienen un polinomio del mismo grado (grado \(3\)), su comportamiento es similar cuando \(x\) toma valores grandes, como se observa en sus gráficas:
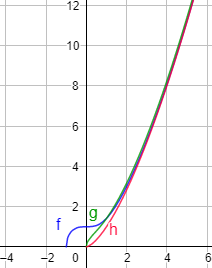
Podríamos decir que las funciones son casi iguales:
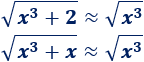
Esto nos facilita el cálculo de límites: los tres límites de estas funciones coinciden:
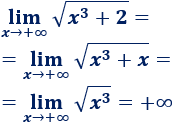
Nota: no hay que aplicar este procedimiento cuando tenemos una resta de raíces. Observad también que las tres raíces son cuadradas (si son de distinto orden, el razonamiento cambia un poco).
Más información sobre esta técnica para calcular límites en infinitésimos equivalentes.
3. Límites de cocientes de raíces
A continuación, explicamos cómo aplicar el apartado anterior para calcular límites de cocientes de raíces.
Ejemplo 1
Supongamos que tenemos un cociente de raíces de distinto orden:
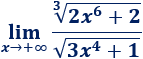
Cuando \(x\) tiende a \(+\infty\), los radicandos tienden a infinito y, por tanto, tenemos un cociente de infinitos:
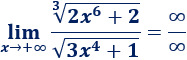
Sin embargo, podemos cambiar las raíces por raíces casi iguales, según vimos anteriormente:
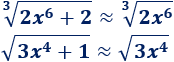
Además, podemos aplicar las propiedades de las raíces/potencias:
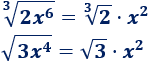
Por tanto, podemos ver el límite inicial como un cociente de polinomios:
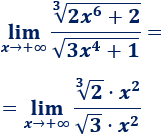
Recordad que el límite del cociente de dos polinomios del mismo grado es igual al cociente de sus coeficientes principales:
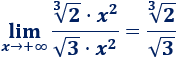
Por tanto,
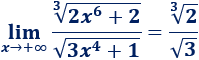
Problema 2
Calcular los siguientes límites de cocientes de raíces de distinto orden:
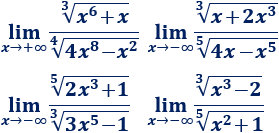
Solución:
Primer límite
Omitimos los monomios de grado menor y simplificamos:
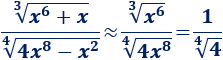
Por tanto,
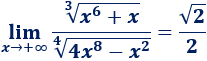
Nota: hemos simplificado la raíz cuarta del siguiente modo:
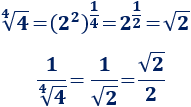
Segundo límite
Primero, observad que \(x\) tiende a infinito negativo. Esto no es un problema porque las raíces son de orden impar.
Procediendo como anteriormente,
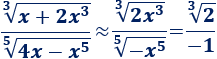
Por tanto,
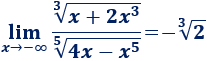
Tercer límite
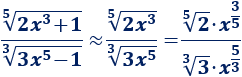
Como el grado es mayor en el denominador, el límite es \(0\):
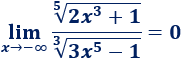
Cuarto límite
Primero, observad que \(x\) tiende a infinito negativo.
Procediendo como anteriormente,
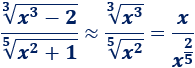
El grado del numerador es mayor, así que el límite es infinito. Observad que, por un lado, la raíz del numerador es cúbica y el grado del monomio principal es \(3\), así que el infinito del numerador es negativo. Por otro lado, el monomio del denominador tiene exponente par, así que el infinito del denominador es positivo.
Por la regla de los signos, el límite es infinito negativo:
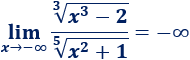
Nota: si, por ejemplo, el exponente del monomio del denominador fuese \(3\) (impar), el resultado del límite cambiaría de signo (por la regla de los signos):
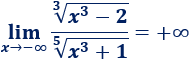
4. Límites de restas de raíces
Recordamos la fórmula de la suma por diferencia:
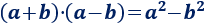
Operando, obtenemos la siguiente fórmula:
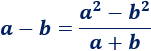
Esta fórmula es de ayuda para resolver límites de restas de raíces cuadradas.
Ejemplo 2
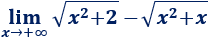
En un principio, tenemos la indeterminación infinito menos infinito. Sin embargo, podemos aplicar la fórmula anterior para evitarla.
Sean
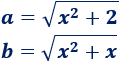
Aplicando la fórmula,
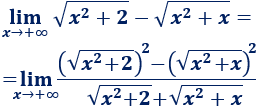
Las raíces del numerador desaparecen por estar elevadas al cuadrado:
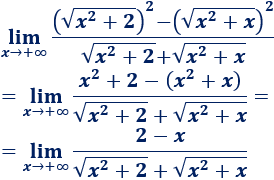
Procediendo como vimos anteriormente, cuando \(x\) es grande, la función del límite es similar a
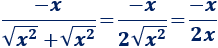
Por tanto,
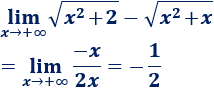
La fórmula anterior sólo nos sirve cuando tenemos una resta de raíces cuadradas. Para las cúbicas, tenemos la fórmula
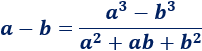
Problema 3
Calcular los siguientes límites de restas de raíces:
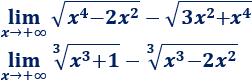
Solución:
Para resolver el primer límite, aplicamos la fórmula de la diferencia cuadrados, es decir,
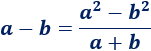
De este modo,
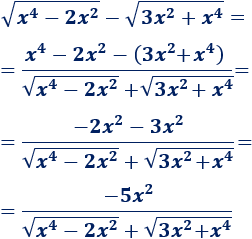
Esta función es casi igual si omitimos los dos monomios de segundo grado del denominador:
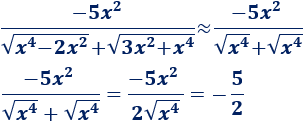
Por tanto, el límite es
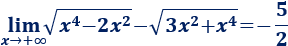
Para resolver el segundo límite, usamos la fórmula de la diferencia de los cubos, es decir,
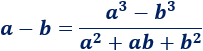
De este modo, el numerador sería
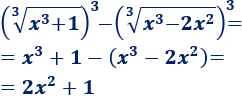
Y el denominador sería
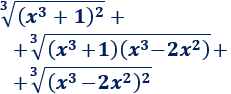
Desarrollamos los radicandos:
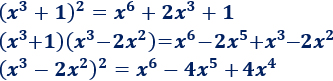
Si nos quedamos con los monomios de mayor grado, el denominador es casi igual a
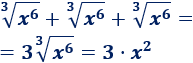
Por tanto,
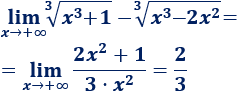
Más problemas similares: