Suma por diferencia
Índice:
- Fórmula
- Ejemplos
- Demostración
- Más ejemplos
1. Fórmula
Se conoce como suma por diferencia a la siguiente fórmula para calcular el producto de dos binomios conjugados:
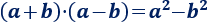
Es decir, el el producto de una suma por una diferencia es igual a la diferencia de sus cuadrados.
La fórmula permite el calcular el producto rápidamente.
2. Ejemplos
Ejemplo 1
Multiplicamos los binomios \(1+x\) y \(1-x\) aplicando la fórmula:
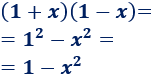
Ejemplo 2
Multiplicamos los binomios \(x-2\) y \(x+2\) aplicando la fórmula:
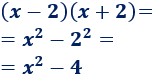
3. Demostración
Para demostrar la fórmula es suficiente con calcular el producto:
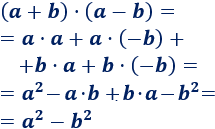
En la última línea hemos utilizado la propiedad conmutativa del producto: \(a·b = b·a\).
Nota: el hecho de que la demostración utilice la propiedad conmutativa del producto implica que la fórmula no sirve cuando no exista dicha propiedad, como es el caso de las matrices.
4. Más ejemplos
Ejemplo 3
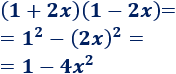
Observad que el segundo sumando es un producto, así que hemos aplicado la propiedad potencia de un producto:
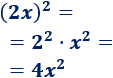
Ejemplo 4
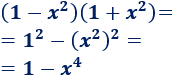
Recordad que la potencia de una potencia se calcula multiplicando los exponentes. Por eso,
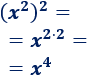
Ejemplo 5
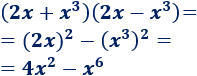
Más problemas similares: productos notables.