Problemas resueltos de
progresiones geométricas
En esta página repasamos los conceptos y fórmulas de las progresiones geométricas y resolvemos algunos problemas.
Índice:
- Progresión, términos, razón y monotonía
- Término o fórmula general
- Suma de los primeros términos
- Suma de todos los términos
- Problemas resueltos
1. Progresión, términos, razón y monotonía
Una progresión geométrica (o sucesión geométrica) es una secuencia ordenada de números llamados términos, de modo que cada término se calcula multiplicando (o dividiendo) un número (llamado razón) al término anterior.
Ejemplo
La sucesión de las potencias de \(2\) es
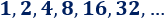
- El primer término es \(a_1 = 1\).
- El segundo término es \(a_2 = 2\).
- El tercer término es \(a_3 = 4\).
- El cuarto término es \(a_4 = 8\).
La razón de esta sucesión es \(r = 2\). Observad que cada término es el resultado de multiplicar por \(2\) al término anterior:
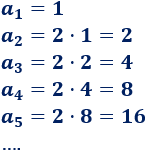
Cada número de la progresión se denomina término. Escribimos \(a_n\) para indicar el término \(n\)-ésimo de la progresión, es decir, el término de la posición \(n\).
Razón:
La razón de una progresión geométrica suele denotarse por \(r\) y se calcula dividiendo un término entre el término anterior:
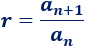
La razón en de una progresión geométrica es constante. Es decir, la división entre dos términos consecutivos siempre tiene que ser la misma.
Por ejemplo, calculamos la razón de la progresión del ejemplo anterior (potencias de \(2\)):
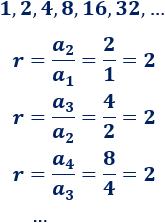
Monotonía:
- Una progresión es monótona creciente si cada término es mayor o igual que el término anterior:
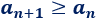
- Una progresión es monótona decreciente si cada término es menor o igual que el término anterior:

- Una progresión es constante si todos los términos son iguales. Esto ocurre cuando la razón es \(r = 1\).
- Una progresión es alternada cuando cada término tiene el signo contrario que el término anterior. Esto ocurre cuando la razón es negativa (\(r< 0\)).
Más información sobre la monotonía en sucesiones geométricas.
2. Término o fórmula general
Llamamos término general a la fórmula que proporciona el término \(n\)-ésimo de una progresión. En las progresiones geométricas es la fórmula
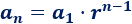
Así, si conocemos el primer término \(a_1\) y la razón \(r\), podemos calcular cualquier término de la progresión.
Ejemplo
El término general de la progresión de los ejemplos anteriores (potencias de \(2\)) es
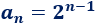
Por ejemplo, calculamos el tercer y sexto término de la sucesión:
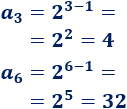
3. Suma de los primeros términos
Podemos calcular la suma de los primeros \(n\) términos de una progresión geométrica mediante la fórmula
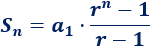
Ejemplo
Calculamos la suma de los \(8\) primeros términos de la progresión de las potencias de \(2\):
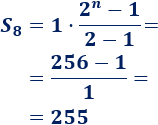
Comprobamos el resultado:
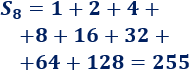
4. Suma de todos los términos
Si una progresión geométrica tiene una razón \(r\) entre \(-1\) y \(1\) (es decir, \(|r|< 1\)), podemos sumar todos los términos de la progresión mediante la fórmula
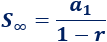
Ejemplo
La progresión de razón \(r = 0.5\) y cuyo primero término es \(a_1 = 12\) es

Cada término se obtiene dividiendo el término anterior entre \(2\).
Como la razón de esta progresión es \(|r|<1\), podemos sumar todos sus términos:
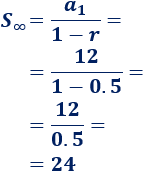
Por tanto, la suma de los infinitos términos de esta sucesión es igual a \(24\).
5. Problemas resueltos
Problema 1
¿Son geométricas las siguientes progresiones? En caso afirmativo, ¿cuáles son sus razones?

Solución:
\( 1\), \( 2\), \(3\), \(4\), \(5\), …
No es una progresión geométrica porque no obtenemos la misma razón si dividimos distintos términos. Por ejemplo,
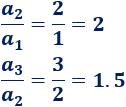
Cada término se obtiene sumando \(1\) al término anterior, así que se trata de una progresión aritmética con diferencia \(d=1\).
\( 1\), \( 3\), \(9\), \(27\), \(81\), …
Es una progresión geométrica con razón \(r = 3\):
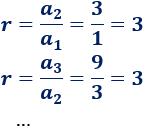
\( 1\), \( 1\), \(1\), \(1\), \(1\) , …
Es una progresión constante (razón \(r=1\)).
\( 1\), \( 2\), \(1\), \(2\), \(1\) , …
No es una progresión geométrica:
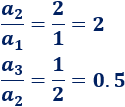
\( 1\), \( -1\), \(1\), \(-1\), \(1\), …
Es una progresión geométrica con razón \(r=-1\):
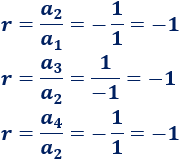
Problema 2
Calcular el término general de las siguientes progresiones geométricas:

Solución:
La fórmula del término general es
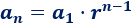
Necesitamos calcular la razón de cada progresión.
\( 1\), \( 5\), \(25\), \(125\), …
La razón es \(r= 5\):
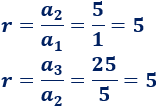
El término general es
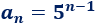
\( 4\), \( 2\), \(1\), \(0.5\), …
La razón es \(r= 1/2\):
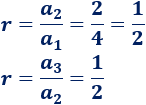
El término general es
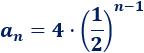
Si aplicamos las propiedades de las potencias,
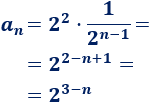
\( 2\), \( -4\), \(8\), \(-16\), …
La razón es \(r= -2\):
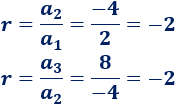
El término general es
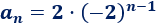
Problema 3
Calcular la suma de los primeros \(5\) términos de la progresión geométrica con razón \(r = 0.5\) y cuyo primero término es \(a_1 = 16\).
Solución:
Usamos la fórmula para sumar los primeros términos:
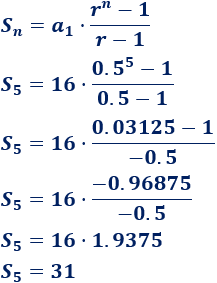
Problema 4
El tercer término de una progresión geométrica es \(a_3 = -25\) y la razón es \(r=-5\). ¿Cuál es el primer término?
Solución:
El término general es
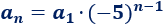
Sustituyendo \(n=3\),
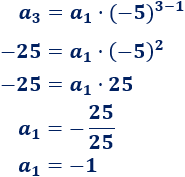
El primer término es \(a_1 = -1\).
Problema 5
El quinto y el sexto término de una progresión geométrica son \(a_5 = 80\) y \(a_6 = 160\). ¿Cuál es el primer término?
Solución:
Como los términos son consecutivos, podemos calcular la razón fácilmente:
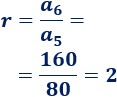
La fórmula del término general es
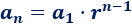
Como conocemos \(r = 2\) y \(a_5 = 80\), podemos calcular \(a_1\):
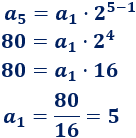
El primer término de la progresión es \(a_1 = 5\).
Problema 6
El segundo y el cuarto término de una progresión geométrica son \(a_2 = 4.5\) y \(a_4 = 10.125\). ¿Cuál es el primer término?
Solución:
Sea \(r\) la razón de la progresión. Entonces, el tercer término es
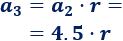
Y el cuarto término es
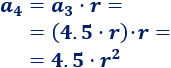
Como sabemos que \(a_4 = 10.125\), tenemos
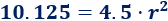
Resolvemos la ecuación cuadrática incompleta:
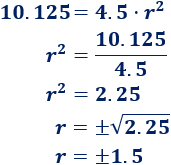
Tenemos dos posibles razones: \(r = 1.5\) y \(r = -1.5\).
Usando el término general,
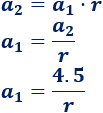
- Si \(r = 1.5\), entonces el primer término es
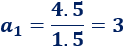
- Y si \(r = -1.5\), el primer término es
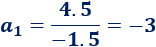
Tenemos dos soluciones porque hay dos progresiones geométricas que cumplen que \(a_2 = 4.5\) y \(a_4 = 10.125\):
- \(3\), \(4.5\), \(6.75\), \(10.125\),…
- \(-3\), \(4.5\), \(-6.75\), \(10.125\),…
Problema 7
El primer y el tercer término de una progresión geométrica son \(a_1 = -2\) y \(a_3= -2\). ¿Cuál es la razón?
Solución:
Sea \(r\) la razón de la progresión.
El segundo término es
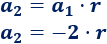
El tercer término es
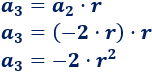
Como \(a_3 = -2\), entonces
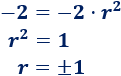
Tenemos dos posibles soluciones: \(r = 1\) y \(r=-1\). Esto es porque hay dos progresiones geométricas cuyos primer y tercer términos son iguales a \(-2\):
- La progresión constante \(-2\), \(-2\), \(-2\), …
- La progresión alternada \(-2\), \(2\), \(-2\),…
Problema 8
El lunes Jaime cuenta un secreto a \(5\) amigos. Al día siguiente, estos \(5\) amigos cuentan el secreto a otros \(5\) amigos. Al día siguiente, las nuevas personas que saben el secreto también lo cuentan a otras \(5\) personas. Y, así, sucesivamente.
Suponiendo que cada persona sólo ha contado el secreto a otras \(5\), ¿cuántas personas saben el secreto el domingo?
Solución:
Construimos una sucesión: el término \(a_n\) es el número de personas que descubren el secreto en el día número \(n\).
El primer día sólo Jaime conoce el secreto:
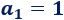
El segundo día, Jaime cuenta el secreto a \(5\) amigos:
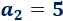
El tercer día, cada uno de los \(5\) amigos cuenta el secreto a otros \(5\), así que el número de personas que se enteran es

Y así, sucesivamente.
Se trata de una progresión geométrica con razón \(r = 5\).
El número de personas que saben el secreto el domingo es \(S_7\). Lo calculamos:
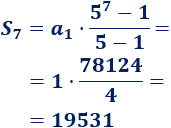
Problema 9
Una sucesión geométrica con primer término \(a_1 = 2\) tiene razón \(r = 0.3\). ¿Cuál es la suma de los \(6\) primeros términos? ¿Y la suma de todos sus términos?
Solución:
Calculamos la suma de los \(6\) primeros términos:
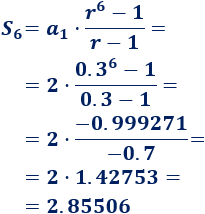
Como la razón es \(|r|<1\), podemos sumar todos los términos de la sucesión:
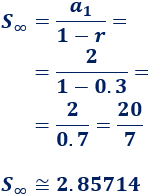
Problema 10
La suma de los primeros \(5\) términos de una progresión geométrica con razón \(r = -2\) es \(S_5 =-77\). ¿Cuál es el primer término?
Solución:
La suma de los \(5\) primeros términos es
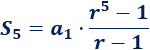
Como sabemos que \(S_5 = -77\) y que \(r = -2\),
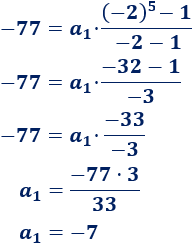
Más problemas de progresiones:
- Test básico sobre progresiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones
- Tipos de progresiones
- Operaciones con sucesiones
- Sucesión de Fibonacci
- Otros temas y calculadoras de progresiones