Problemas resueltos de
progresiones aritméticas
En esta página repasamos los conceptos y fórmulas básicas de las sucesiones o progresiones aritméticas y resolvemos \(15\) problemas.
Índice:
- Progresión, términos y diferencia
- Monotonía (creciente o decreciente)
- Término o fórmula general
- Suma de los primeros términos
- 15 problemas resueltos
1. Progresión, términos y diferencia
Una progresión aritmética (o sucesión aritmética) es una secuencia ordenada de números llamados términos, de modo que cada término se calcula sumando (o restando) un número (llamado diferencia, \(d\)) al término anterior.
Ejemplo
La sucesión de los números impares es

- El primer término es \(a_1 = 1\).
- El segundo término es \(a_2 = 3\).
- El tercer término es \(a_3 = 5\).
- El cuarto término es \(a_4 = 7\).
La diferencia de esta sucesión es \(d = 2\). Observad que cada término es el resultado de sumarle \(2\) al término anterior:
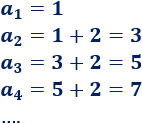
Cada número de la progresión se denomina término. Escribimos \(a_n\) para indicar el término \(n\)-ésimo de la progresión, es decir, el término de la posición \(n\).
La diferencia suele denotarse por la letra \(d\) y se calcula restando dos términos consecutivos:
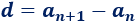
La diferencia es constante en toda la progresión, así que no importa qué par de términos restamos para calcularla, siempre que sean consecutivos: cualquier término menos el término que le precede.
2. Monotonía (creciente o decreciente)
- Si la diferencia es positiva, \(d>0\), cada término es mayor que el anterior. Se dice que es una progresión monótona creciente.
- Si la diferencia es negativa, \(d<0\), cada término es menor que el anterior. Se dice que es una progresión monótona decreciente.
- Si la diferencia es \(d=0\), todos los términos son iguales. Se dice que es una progresión constante.
Ejemplo
- La progresión \(1\), \(3\), \(5\), \(7\),... tiene diferencia \(d=2 >0\). Es montóna creciente.
- La progresión \(10\), \(8\), \(6\), \(4\),... tiene diferencia \(d=-2 <0\). Es monótona decreciente.
- La progresión \(1\), \(1\), \(1\), \(1\),... es constante.
3. Término o fórmula general
Llamamos término general a la fórmula que proporciona el término \(n\)-ésimo de la sucesión:
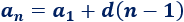
Si conocemos el primer término \(a_1\) y la diferencia \(d\), podemos calcular cualquier término.
Ejemplo
La progresión de los números impares (\(1\), \(3\), \(5\), \(7\),...) tiene diferencia \(d=2\) y su primer término es \(a_1=1\), así que el término general es
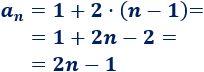
Calculamos los términos \(a_3\), \(a_5\) y \(a_9\) a partir del término general:

4. Suma de los primeros términos
Podemos calcular la suma de los primeros \(n\) términos de una progresión aritmética mediante la fórmula
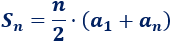
La progresión de los números pares es
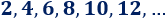
Calculamos la suma de los \(5\) primeros términos mediante la fórmula:
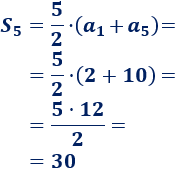
En efecto, podemos comprobar que la suma es \(30\):
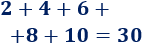
5. Problemas resueltos
Problema 1
Determinar si las siguientes progresiones son aritméticas:

En caso afirmativo, calcular la diferencia de cada progresión.
Solución:
\(1,\ 4,\ 7,\ 10,\ 13,\ …\)
Es aritmética porque cada término se obtiene sumando \(3\) al anterior:
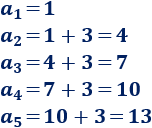
La diferencia es \(d = 3\).
\(1,\ 0,\ 1,\ 0,\ 1,\ …\)
No es aritmética porque el segundo término se obtiene restando \(1\) al primer término, pero el tercer término se obtiene sumando \(1\).
Para que sea aritmética, tenemos que, o bien sumar, o bien restar, el mismo número en toda la progresión.
\(1,\ 0,\ -1,\ -2,\ -3,\ …\)
Es aritmética porque cada término es el resultado de restarle \(1\) al anterior:
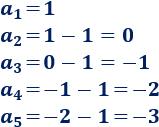
La diferencia es \(d=-1\).
\(1,\ 3,\ 6,\ 10,\ 15,\ …\)
No es aritmética porque el segundo término se calcula sumando \(2\) al primero pero, por ejemplo, el quinto término se calcula sumando \(5\) al cuarto.
\(1,\ 2,\ 3,\ 4,\ 5,\ …\)
Es aritmética porque cada término se calcula sumando \(1\) al término anterior:
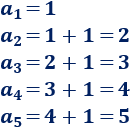
La diferencia es \(d=1\).
Problema 2
Calcular los \(5\) primeros términos de la sucesión aritmética cuyo término general es

Solución:
Sólo tenemos que dar valores a \(n\) en la fórmula:
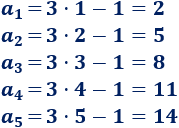
Problema 3
El término general de una sucesión aritmética es

¿Cuál es la diferencia de esta sucesión?
Solución:
Podemos calcular dos términos consecutivos y restarlos.
Calculamos \(a_1\) y \(a_2\):
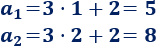
Calculamos la diferencia:
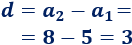
Problema 4
El término general de una sucesión aritmética es
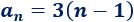
¿Cuál es la diferencia de esta sucesión?
Solución:
Calculamos los dos primeros términos:
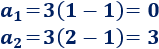
Calculamos la diferencia:
Problema 5
El término general de una sucesión aritmética es

¿Cuál es la diferencia de esta sucesión?
Solución:
Calculamos los dos primeros términos:
Calculamos la diferencia:
Problema 6
El término general de una sucesión aritmética es
¿Cuál es la suma de sus \(4\) primeros términos?
Solución:
La fórmula para sumar los \(n\) primeros términos es
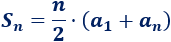
Calculamos \(a_1\) y \(a_4\) usando el término general:
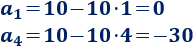
Sumamos los \(4\) primeros términos:
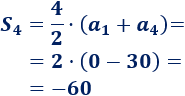
Problema 7
Calcular la diferencia y el término general de las siguientes progresiones aritméticas:
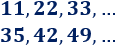
Solución:
La diferencia se calcula restando dos términos consecutivos:
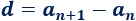
El término general es
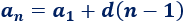
\(11,\ 22,\ 33,\ …\)
Calculamos la diferencia restando dos términos:
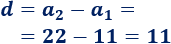
Como el primer término es \(a_1=11\) y la diferencia es \(d=11\), el término general es
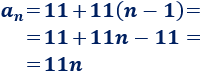
\(35,\ 42,\ 49,\ …\)
Calculamos la diferencia:
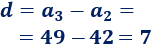
Como el primer término es \(35\), el término general es
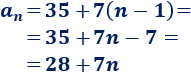
Problema 8
Calcular la suma de los primeros \(5\) términos de las siguientes progresiones:
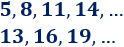
Solución:
La fórmula de la suma de los \(n\) primeros términos es
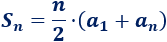
Necesitamos el primer y el quinto término.
\(5,\ 8,\ 11,\ 14,\ …\)
La diferencia de esta sucesión es \(d = 3\), así que el quinto término es
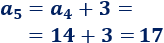
Calculamos la suma:
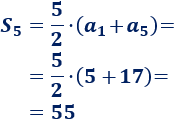
\(13,\ 16,\ 19,\ …\)
La diferencia de esta sucesión es \(d = 3\), así que el cuarto y quinto términos son
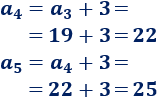
Calculamos la suma:
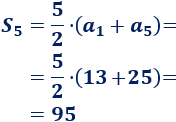
Problema 9
Alberto tiene un armario con \(10\) cajones numerados del \(1\) al \(10\) y guarda \(n\) objetos en el cajón número \(n\).
Después de haber usado los \(10\) cajones, ¿cuántos objetos ha guardado Alberto en total?
Solución:
Se trata de una progresión aritmética: si \(a_n\) es el número de objetos en el cajón número \(n\), tenemos la progresión cuyo término general es

Tenemos que sumar los \(10\) primeros términos de la sucesión:
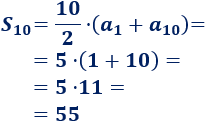
Alberto ha guardado un total de \(55\) objetos.
Problema 10
Los primeros términos de la llamada sucesión de Fibonacci son los siguientes:
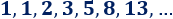
¿Es una sucesión aritmética? En caso afirmativo, ¿cuál es la diferencia?
Solución:
No es una progresión aritmética porque no hay una diferencia constante en toda la progresión.
Por ejemplo, si restamos los dos primeros términos,
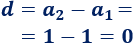
Sin embargo, si restamos los términos segundo y tercero y los términos tercero y cuarto, obtenemos \(d=1\):
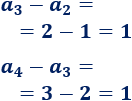
Y si restamos los términos cuarto y quinto, obtenemos \(d=2\):
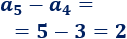
Por tanto, no se trata de una progresión aritmética.
Problema 11
El sexto término de una sucesión aritmética es \(a_6 = 36\) y el séptimo término es \(a_7 = 42\). ¿Cuál es el primer término de la sucesión? ¿Y la diferencia?
Solución:
Como conocemos los términos sexto y séptimo, que son consecutivos, podemos calcular la diferencia:
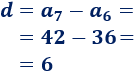
Vamos a usar la fórmula del término general:
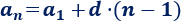
Como sabemos que \(a_6 = 36\) y que \(d=6\), entonces, sustituyendo \(n=6\) en la fórmula,
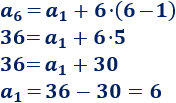
Por tanto, el primer término es \(a_1 = 6\).
Problema 12
El tercer término de una sucesión aritmética es \(a_3 = 14\) y el quinto término es \(a_5 = 20\). ¿Cuál es el primer término de la sucesión? ¿Y la diferencia?
Solución:
El término \(a_4\) se obtiene sumando la diferencia \(d\) al término \(a_3\):
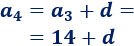
Razonando igual, el quinto término es
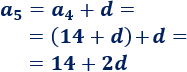
Como sabemos que \(a_5=20\), entonces
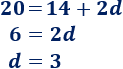
Por tanto, la diferencia es \(d=3\).
Usamos la fórmula del término general:
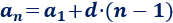
Como sabemos que \(a_3 = 14\) y que \(d = 3\), sustituyendo \(n=3\) en el término general tenemos
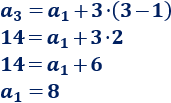
El primer término de la progresión es \(a_1 = 8\).
Problema 13
El quinto término de una sucesión aritmética es \(a_5 = 45\) y la suma de los \(5\) primeros términos de la sucesión es \(S_5 = 115\). ¿Cuál es el primer término?
Solución:
La fórmula de la suma de los primeros \(n\) términos es
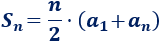
Como sabemos que \(S_5 = 115\) y que \(a_5=45\), sustituyendo en la fórmula,
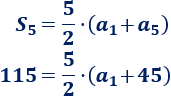
Multiplicamos la ecuación por \(2\):
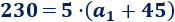
Dividimos la ecuación entre \(5\):
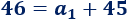
La solución de la ecuación es
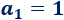
Por tanto, el primer término es \(a_1 = 1\).
Problema 14
El primer término de una sucesión aritmética es \(a_1 = 3\) y la suma de los \(5\) primeros términos de la sucesión es \(S_5 = 25\). ¿Cuál es el quinto término?
Solución:
La fórmula de la suma de los \(5\) primeros términos es
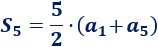
Sustituimos \(S_5 = 25\) y \(a_1 = 3\):
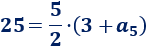
Con esta ecuación podemos calcular el quinto término:
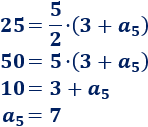
Por tanto, el quinto término es \(a_5 = 7\).
Problema 15
El quinto término de una sucesión aritmética es \(a_5 = 0\) y su diferencia es \(d = -3\).
¿Cuál es la suma de los \(5\) primeros términos de la sucesión?
Solución:
La fórmula de la suma de los \(5\) primeros términos es
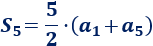
Como conocemos \(a_5\), necesitamos calcular \(a_1\).
El término general es
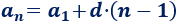
Como \(d=-3\) y \(a_5 =0\), tenemos
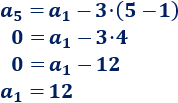
Ya podemos calcular la suma:
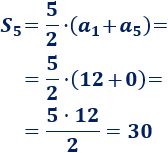
Por tanto, los \(5\) primeros términos suman \(30\).
Más problemas de progresiones:
- Test básico sobre progresiones
- Progresiones aritméticas
- Progresiones geométricas
- Problemas de progresiones
- Tipos de progresiones
- Operaciones con sucesiones
- Sucesión de Fibonacci
- Otros temas y calculadoras de progresiones