Progresión aritmética de segundo orden
En esta página recordamos el concepto de progresión aritmética (de primer orden); definimos progresión aritmética de segundo orden, proporcionamos la fórmula para sumar sus primeros términos y resolvemos algunos problemas.
Índice:
- Introducción
- Definición y diferencia
- Suma de los primeros términos
- Problemas resueltos
1. Introducción
Una progresión aritmética de primer orden es una progresión cuyo término general es un polinomio de primer grado:
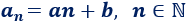
siendo \(a\) y \(b\) constantes.
La diferencia entre dos términos consecutivos, \(d\), es una constante llamada diferencia:
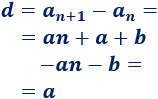
Ejemplo
La progresión de los números impares \(1\), \(3\), \(5\), \(7\),… tiene diferencia \(d = 2\) y su término general es

2. Definición y diferencia
Una progresión aritmética de segundo orden es una progresión cuyo término general es un polinomio de segundo grado:
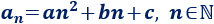
siendo \(a\), \(b\) y \(c\) constantes.
La diferencia entre dos términos consecutivos no es constante, sino una progresión aritmética de primer orden:
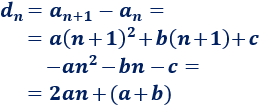
La diferencia de la progresión \(d_n\) es \(d = 2a\):
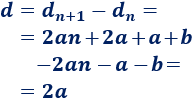
Ejemplo
La siguiente progresión es aritmética de segundo orden:
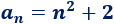
Los primeros términos son
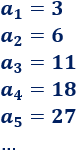
La sucesión diferencia de la sucesión es
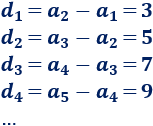
Es decir, es una progresión aritmética con diferencia \(2\) cuyo término general es

3. Suma de los primeros términos
Sea \(S_n\) la suma de los primeros términos de la progresión aritmética de segundo orden \(a_n\):
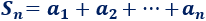
Se puede calcular esta suma mediante la siguiente fórmula:
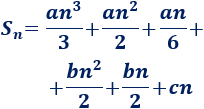
Ejemplo
Calculamos la suma de los \(5\) primeros términos de la sucesión del ejemplo anterior (\(a_n = n^2+2\)) mediante la fórmula:
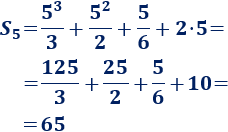
La demostración de la fórmula es sencilla ya que la suma a calcular es
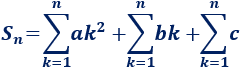
Y sabemos que el primer sumatorio es
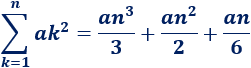
El segundo es
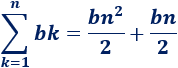
Y el tercero es
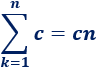
4. Problemas resueltos
Problema 1
Hallar el término general de la progresión formada por los cuadrados de la progresión de los números impares (\(1\), \(3\), \(5\), \(7\),…).
Solución:
Él término general de la sucesión de los números impares es

La sucesión de sus cuadrados es
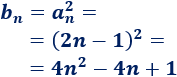
Se trata de una progresión aritmética de segundo orden.
Problema 2
Hallar la diferencia de la progresión formada por los cuadrados de la progresión de los números pares (\(0\), \(2\), \(4\), \(6\),…).
Solución:
El término general de la progresión de los pares es

La progresión de sus cuadrados es
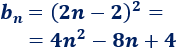
Calculamos la diferencia de la progresión:
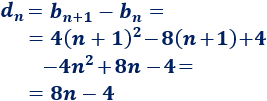
Problema 3
El tercer término de una progresión aritmética de segundo orden es \(a_3 = 21\) y su diferencia es \(d_n = 4n+3\). ¿Cuál es su término general?
Solución:
El término general tiene la forma
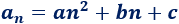
Calculamos los términos \(d_1\) y \(d_2\):
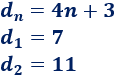
Los primeros términos de la progresión \(a_n\) son
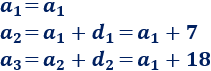
Conocemos \(a_3 = 21\):
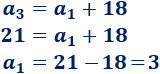
Usando el término general \(a_n\),
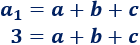
Como conocemos \(a_1\), el segundo término es
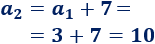
Usando el término general \(a_n\),
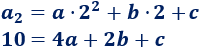
Usando el término general \(a_n\),
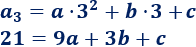
Tenemos un sistema de ecuaciones:
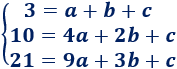
La solución del sistema es
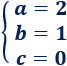
Por tanto, el término general de la progresión aritmética de segundo orden es

Más problemas similares: Problemas y calculadoras de progresiones.