Integral definida y áreas
Recordamos la regla de Barrow y explicamos cómo utilizarla para calcular el área de la región que encierran la gráfica de una función y el eje de abscisas o el área que encierran las gráficas de dos funciones. Con ejemplos y problemas resueltos.
Índice:
- Regla de Barrow
- Área entre una gráfica y el eje X
- Área entre dos gráficas
- Problemas resueltos
1. Regla de Barrow
Supongamos que \(F\) es una primitiva de \(f\), es decir,
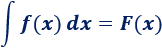
La regla de Barrow establece que
2. Área entre una gráfica y el eje X
Las aplicaciones de la integral definida son variadas, siendo el cálculo de áreas una de ellas.
Caso 1
Si la función \(f\) es no negativa en el intervalo \([a,b]\), entonces su integral definida es el área que encerrada entre su gráfica y el eje OX:
La representación corresponde a la gráfica de la función
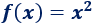
El área que encierra su gráfica con el eje X en el intervalo \([0,2]\) es la siguiente integral definida:
Caso 2
Si la función \(f\) es no positiva en el intervalo \([a,b]\), entonces su integral definida es el área encerrada entre su gráfica y el eje X, pero con valor negativo:
La representación corresponde a la gráfica de la función
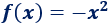
El área que encierra su gráfica con el eje X en el intervalo \([0,2]\) es el valor absoluto de la integral definida:
Caso 3
Recordad la siguiente propiedad de las integrales definidas para \(a\leq b\leq c\):
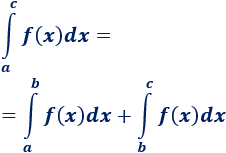
Si la función \(f\) es negativa y positiva, la región que encierra su gráfica con el eje X está dividida en varias regiones, algunas sobre el eje y otras bajo éste:
La representación corresponde a la gráfica de la función
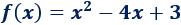
El área que encierra su gráfica con el eje OX en el intervalo \([0,2]\) esta dividida en dos regiones. Su área es
Tenemos que calcular una integral para cada región porque en la región que está bajo el eje, la integral es negativa.
La primera integral es
La segunda es
Por tanto, el área total de la región es
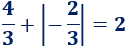
3. Área entre dos gráficas
Consideremos el área de la región encerrada entre las gráficas de dos funciones:
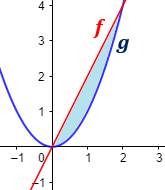
Son las gráficas de las funciones
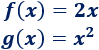
Estas gráficas intersectan en los puntos
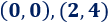
Es fácil ver que el área que encierran viene dada por la integral definida
Observad que en la integral hemos escrito \(f-g\) porque la gráfica de \(f\) está por encima de la de \(g\): el área corresponde al área que encierra la gráfica de \(f\) con el eje X menos el área que encierra la de \(g\) con el eje X.
Además, el área corresponde con la integral porque la región está situada sobre el eje X. De no ser así, debemos calcular el área con un valor absoluto y/o con varias integrales.
4. Problemas resueltos
Problema 1
Calcular el área de la región encerrada entre la gráfica de \(f\) y el eje X en el intervalo \([-1,1]\):
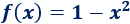
Solución:
Las raíces de la función son \(x=\pm 1\). Además, es una parábola con forma de \(\cap\). La región está sobre el eje X y podemos calcular su área con una única integral definida.
Además, la parábola es simétrica respecto del eje Y, así que el eje Y divide la región en otras dos regiones de igual área.
El área total es
Nota: en este caso, nos interesa aprovechar la simetría porque así uno de los extremos de la integral es \(0\), lo cual siempre facilita los cálculos.
Problema 2
Calcular el área de la región encerrada entre la gráfica de \(f\) y el eje X en el intervalo \([-1,1]\):
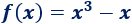
Solución:
La función tiene \(3\) raíces en el intervalo dado, así que tendremos la región divida por el eje X:
En un principio, tenemos que calcular dos integrales definidas. Una tiene signo positivo y la otra, negativo. Sin embargo, observad que la función tiene simetría (rotacional), por lo que será suficiente duplicar el resultado de una de las dos integrales.
El área total es
Problema 3
Calcular el área de la región encerrada entre la gráfica de \(f\) y las rectas \(x=-1\) y \(x=2\):
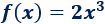
Solución:
Representamos la gráfica y las rectas:
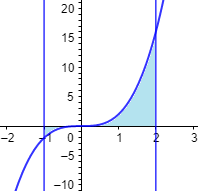
En este caso, las dos regiones no tienen la misma área y, además, cada una tiene un signo distinto, por lo que tenemos que calcular dos integrales definidas.
El área de la región del lado izquierdo es
La del lado derecho es
El área total es \(17/2\).
Problema 4
Calcular el área de la región delimitada por las gráficas de las funciones
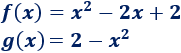
Solución:
Representamos las gráficas:
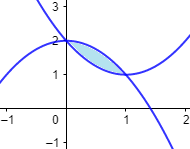
La gráfica superior es la de \(g\) (en toda la región) y la región está sobre el eje X, así que no hay ninguna complicación.
Lo único que tenemos que calcular son los puntos de intersección igualando ambas funciones:
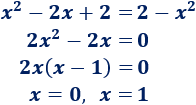
Los puntos de intersección son \(x=0\) y \(x=1\).
La diferencia \(g-f\) es
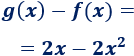
El área de la región es
Problema 5
Calcular el área de la región delimitada por las gráficas de las funciones
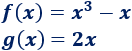
Solución:
Representamos las gráficas:
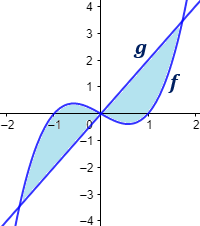
Hay simetría rotacional: el área de la región del lado izquierdo coincide con la del lado derecho. Por tanto, es suficiente con calcular una de ellas.
Observad que el área (del lado derecho) está dividida por el eje X. Dividimos la región en \(3\):
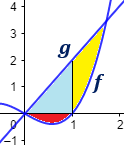
Color rojo: es el valor absoluto de la integral definida de \(f\) en el intervalo \([0,1]\):
Color azul: es la integral definida de \(g\) en el intervalo \([0,1]\):
Color amarillo: es la integral definida de \(g-f\) en el intervalo \([1,a]\).
El extremo \(a\) es la intersección de las gráficas. Lo calculamos:
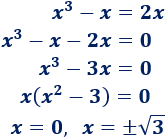
Por tanto, \( a = \sqrt{3}\).
Luego el área de la región amarilla es
Por tanto, el área del lado derecho de la región es
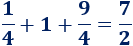
El área total de la región es el doble, es decir, \(7\).
Más problemas similares: cálculo de áreas (integral definida).