Moda, media y mediana
La moda, media y mediana son parámetros estadísticos, es decir, son números que se calculan a partir de los datos para estudiarlos en su conjunto.
En esta página explicamos cómo calcular la media, moda y mediana de un conjunto de datos. También, explicamos la diferencia entre la media aritmética y la ponderada. Con ejemplos y problemas resueltos explicados paso a paso.
Índice:
- Moda
- Media (aritmética)
- Mediana
- Media ponderada
- Problemas resueltos
1. Moda
La moda de un conjunto de datos es el dato que más se repite.
Ejemplo: la moda de los datos, 2, 3, 1, 3, 2, 4, 3 es 3, porque es el dato que más se repite.
Si hay varios datos que se repiten el mismo número de veces, entonces hay varias modas.
Ejemplo: la moda de los datos, 1, 2, 1, 2, 3, 4 es 1 y 2.
2. Media (aritmética)
La media de un conjunto de datos se calcula sumando todos los datos y dividiendo el resultado entre el número de datos.
Ejemplo
Las notas de Manuel en el examen de matemáticas fueron: 5, 6, 5, 4, 6 y 4.
Calculamos la suma de los datos:
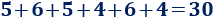
Como hay 6 datos, dividimos el resultado anterior entre 6:
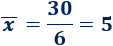
La media de las notas es 5.
Significado: si Manuel hubiese obtenido la misma nota en todos los exámenes, sería la media, que es un 5. Por esta razón, suele usarse la media de todas las notas para la nota de la asignatura.
Normalmente, la media se denota por \(\overline{x}\) y a cada uno de los datos, \(x_i\). De este modo, se puede escribir la media de \(N\) datos como
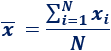
La media que hemos explicado se denomina también media aritmética, para distinguirla de la media ponderada, la cual veremos más adelante.
3. Mediana
La mediana de un conjunto de datos ORDENADOS es el dato que ocupa la posición central.
Ejemplo
La mediana de los datos 1, 2, 3, 1, 2, 3, 1 es 2.
Para calcularla, tenemos que ordenar los datos:

El dato central es 2, así que la mediana es 2.
Si el número de datos es PAR, entonces no hay un dato que sea central. En este caso, se toman los dos datos centrales y se define la mediana como su media.
Ejemplo
La mediana de los datos 1, 2, 3, 1, 3, 1 es 1,5.
Tenemos que ordenar los datos:

Los dos datos centrales son 1 y 2. Calculamos su media:
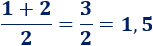
Por tanto, la mediana de los datos es 1,5.
La mediana es el número por debajo y por encima del cual está la mitad de los datos (la mitad por debajo y la mitad por arriba).
4. Media ponderada
En ocasiones, algunos de los datos son más importantes o tienen más peso que los demás, por lo que cuando se calcula la media de los datos, se quiere que estos influyan más en el resultado.
A cada dato \(x_i\) se le asigna un peso \(p_i\) y la media ponderada es
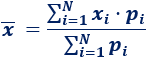
Es decir, se suman los datos multiplicados por su peso y el resultado se divide entre la suma de todos los pesos.
Veamos un ejemplo para comprender este concepto.
Ejemplo
Los alumnos de matemáticas realizan un total de 3 exámenes:
- El examen 1 corresponde a los temas 1, 2 y 3 del temario.
- El examen 2 corresponde a los temas 1, 2, 3, 4, 5 y 6.
- El examen 3 (examen final) corresponde a los temas 1, 2, 3, 4, 5, 6, 7 y 8.
El profesor de matemáticas considera que la nota del examen 2 debe tener más peso que la nota del examen 1, y que la nota del examen 3 debe tener más peso que las notas de los otros dos exámenes. Por esta razón, el profesor asigna un PESO a cada una de los exámenes:
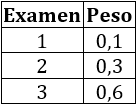
Las notas de Manuel en los tres exámenes son
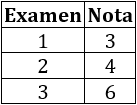
Calculamos la media ponderada (en el numerador, cada nota debe multiplicarse por su peso; en el denominador, se suman todos los pesos):
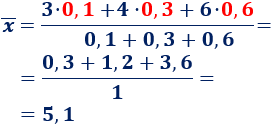
Por tanto, la nota media (ponderada) de Manuel es un 5,1, con lo que aprueba la asignatura de matemáticas.
Si en lugar de la media ponderada, el profesor calcula la media aritmética, la nota de Manuel sería
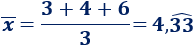
En este caso, Manuel no aprobaría la asignatura, aunque hubiese superado el examen final.
5. Problemas resueltos
Problema 1
La siguiente tabla recoge el número de goles marcados por el equipo de Marcos y el de Manuel durante la temporada:
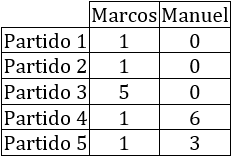
Calcular la media, moda y mediana de los goles que marcó cada equipo.
Solución:
Equipo de Marcos: 1, 1, 1, 1 y 5.
Media:
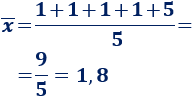
Moda: el que más se repite es 1.
Mediana: el dato de la posición central es 1.
Equipo de Manuel: 0, 0, 0, 3 y 6.
Media:
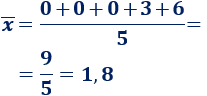
Moda: el que más se repite es 0.
Mediana: el dato de la posición central es 0.
Problema 2
Las alturas (en centímetros) de los componentes de dos grupos de amigos son las siguientes:

Calcular las medias de ambos grupos y comentar los resultados.
- ¿Todos los amigos miden lo mismo?
- ¿En qué grupo está el amigo más alto? ¿Y el más bajo?
- ¿En qué grupo las alturas de los amigos son cercanas a la media?
- ¿Es la media un buen parámetro para estudiar la diferencia o variación que hay entre los datos?
Solución:
Media del grupo 1:
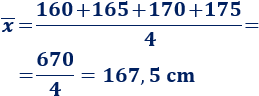
Media del grupo 2:
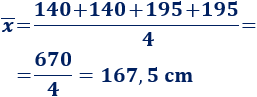
Si todos los amigos del grupo 1 midieran lo mismo, medirían 167,5cm. Lo mismo para el grupo 2.
a. No, solo hay 2 amigos que miden 140 y otros 2 que miden 195. Los demás amigos tienen alturas distintas.
b. El amigo más alto y el más bajo se encuentran en el grupo 2.
c. Los amigos del grupo 1 tienen una altura más cercana a la media del grupo.
d. No, la media NO sirve para estudiar la diferencia que hay entre los datos, puesto que los datos altos se compensan con los bajos. Ambos grupos tienen la misma media, pero las alturas son más cercanas entre sí en el grupo 1 que en el grupo 2.
Problema 3
Notas obtenidas por los 20 alumnos de la asignatura de matemáticas: 3, 8, 3, 5, 4, 7, 9, 3, 9, 10, 7, 4, 6, 7, 7, 8, 2, 7, 8, 6.
- Calcular media, moda y mediana.
- En general, ¿han aprobado la asignatura los alumnos?
Solución:
Ordenamos los datos: 2, 3, 3, 3, 4, 4, 5, 6, 6, 7, 7, 7, 7, 7, 8, 8, 8, 9, 9, 10.
a. Calculamos la media sumando todas las notas y dividiendo el resultado entre 20:
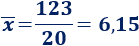
La moda es la nota que más se repite: 7.
La mediana es la nota de la posición central, pero como hay un número par de datos, hay dos notas centrales: 7 y 7. La mediana es su media, que es 7.
Como la mediana es 7, la mitad de las notas son menores o iguales que 7 y la otra mitad son mayores o iguales que 7.
b. Como la mitad de las notas son mayores o iguales que 7 y también hay notas entre 5 y 7, hay más alumnos aprobados que no aprobados. Por tanto, podemos decir que en general han aprobado.
Problema 4
En las oposiciones de profesor de matemáticas, los puntos obtenidos en el examen teórico y en el práctico cuentan el 40% y el 60% respectivamente. La nota final es la media ponderada.
Notas obtenidas por Javier y Marina:
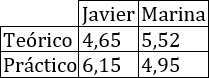
¿Cuál de los dos candidatos obtendrá la única plaza de profesor por tener una nota mayor?
Solución:
Tenemos que calcular la media ponderada de ambos candidatos.
Nota de Javier:
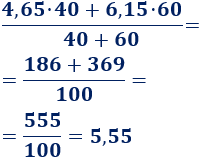
Nota de Marina:
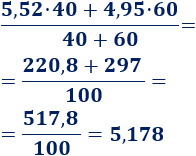
La plaza la obtendrá Javier.