Valor absoluto
Definimos valor absoluto y proporcionamos algunas propiedades, ejemplos y ejercicios resueltos.
Índice:
- Definición y ejemplos
- Función valor absoluto
- Algunas propiedades
- Problemas resueltos
1. Definición y ejemplos
El valor absoluto de un número \(a\) se escribe como \(|a|\) y es su valor numérico sin signo.
Ejemplos
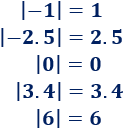
El valor absoluto de \(x\), \(|x|\), es \(-x\) si \(x\) es negativo y es \(x\) si \(x\) es positivo ó \(0\):
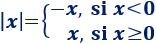
2. Función valor absoluto
La función valor absoluto es la función \(f:\mathbb{R}\to [0,+\infty)\) dada por
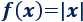
También, podemos definir la función por partes:
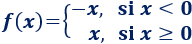
La gráfica de la función es
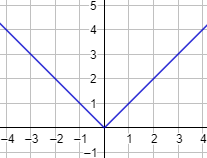
Esta función es continua en todos los reales y derivable en todos los reales excepto en \(x=0\).
3. Algunas propiedades
Veamos algunas de las propiedades más importantes del valor absoluto:
Propiedad 1
El valor absoluto de un número es siempre no negativo:
Propiedad 2
El valor absoluto de un número \(x\) es \(0\) si, y sólo si, \(x=0\):
Propiedad 3
El valor absoluto de un producto es el producto de los valores absolutos de sus factores:
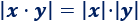
Análogo para el cociente:
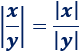
Ejemplo:
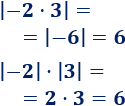
Propiedad 4
Valor absoluto del opuesto:
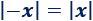
Ejemplo:
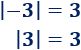
Propiedad 5
Desigualdad triangular (valor absoluto de la suma):
Ejemplo:
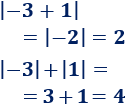
Propiedad 6
Igualdad entre valores absolutos:
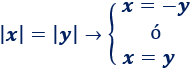
Ejemplo:
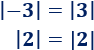
Propiedad 7
Valor absoluto como una raíz:
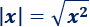
Ejemplo:
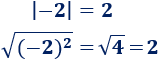
Propiedad 8
Dos propiedades importantes por su aplicación en las inecuaciones:
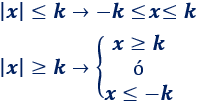
Ejemplo:
Propiedad 9
El valor absoluto como un máximo:
Ejemplo:
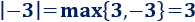
4. Problemas resueltos
Problema 1
Calcular los siguientes valores absolutos:
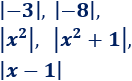
Solución:
El valor absoluto de \(-3\) es \(3\):
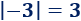
El valor absoluto de \(-8\) es \(8\):
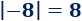
El valor absoluto de \(x^2\) es \(x^2\) porque el cuadrado de cualquier número (real) es no negativo:
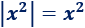
El valor absoluto de \(x^2+1\) es \(x^2+1\) porque \(x^2+1\) siempre es mayor o igual que \(1\):
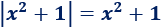
El valor absoluto de \(x-1\) es
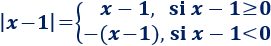
Es decir,
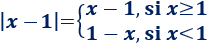
Problema 2
Resolver la siguiente ecuación con valor absoluto:
Solución:
Supongamos que \(x-3\) es mayor o igual que \(0\):
Esto ocurre cuando \(x \geq 3\).
El valor absoluto de \(x-3\) es \(x-3\), así que la ecuación que tenemos es
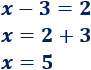
Supongamos ahora que \(x-3\) es menor que \(0\):
Esto ocurre cuando \(x< 3\).
El valor absoluto de \(x-3\) es \(-(x-3)\), así que la ecuación que tenemos es
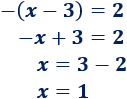
La ecuación tiene dos soluciones: \(x=5\) y \(x=1\).
Problema 3
Demostrar la propiedad siguiente:
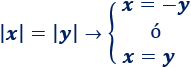
Solución:
Escribimos el valor absoluto en función del signo:
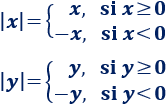
Por tanto, podemos escribir la igualdad de 4 formas posibles:
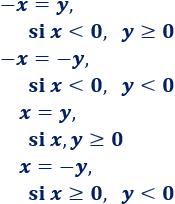
Es decir, \(x=-y\), o bien, \(x = y\).
Problema 4
Resolver la siguiente inecuación con valor absoluto:
Solución:
Por una propiedad que vimos,
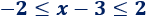
Por un lado, tenemos
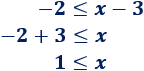
Por otro lado, tenemos
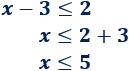
Como deben cumplirse ambas relaciones, las soluciones de la inecuación son las \(x\) mayores o iguales que \(1\) y menores o iguales que \(5\):
Es decir, las soluciones de la ecuación son las \(x\) que cumplen \(1\leq x \leq 5\):
Problema 5
Resolver la siguiente inecuación con valor absoluto:
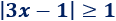
Solución:
Por una propiedad que vimos,
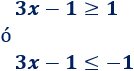
Primer caso:
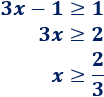
Segundo caso:
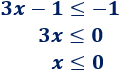
Por tanto, las soluciones de la inecuación son las \(x\) mayores o iguales que \(2/3\) ó las \(x\) menores o iguales que \(0\):
