La raíz cuadrada: √
En esta página definimos la raíz cuadrada de un número (no negativo) y proporcionamos las propiedades de las raíces cuadradas (multiplicación, división y cuadrado de raíces cuadradas). Con ejemplos y problemas resueltos.
Índice:
- Definición y ejemplos
- Producto y cociente de raíces
- Cuadrado de una raíz
- Raíz de un cuadrado
- Problemas resueltos
1. Definición y ejemplos
Definición
La raíz cuadrada de un número \(a\) se escribe como \(\sqrt{a}\) y es el número \(b\) cuyo cuadrado es \(a\), es decir, \(b^2 = a\):

Ejemplos
- 2 es una raíz cuadrada de 4:
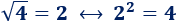
- -2 también es una raíz cuadrada de 4:
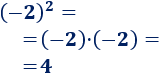
- 3 y -3 son raíces cuadradas de 9:
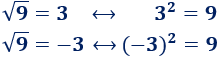
Signo ±
Los números positivos tienen dos raíces cuadradas: el mismo número, pero con signos distintos (+ y -) y, por eso, normalmente se escribe el signo \(\pm\):
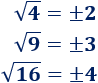
Raíz de un negativo
El cuadrado de un número nunca puede ser negativo por la regla de los signos, así que no tiene sentido considerar la raíz cuadrada de un número negativo.
Ejemplo
La raíz cuadrada de -4 sería el número \(b\) cuyo cuadrado es -4 (es decir, \(b^2 = -4\)), pero no hay un número cuyo cuadrado sea -4:
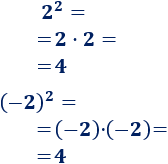
Podemos obtener -4 como el producto \(-2\cdot 2\), pero este producto no es un cuadrado.
Por tanto:
No existen las raíces cuadradas de los números negativos.
Nota: técnicamente, sí existen las raíces de números negativos, pero son números imaginarios, lo cuales se estudian en un nivel más avanzado. Más información en ¿raíces de números negativos?.
2. Producto y cociente de raíces
Producto de raíces
La raíz cuadrada de un producto de números no negativos es el producto de las raíces cuadradas de dichos números:
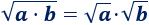
Ejemplo
Raíz cuadrada de 16 como un producto de raíces:

Cociente (fracción) de raíces
La raíz cuadrada de un cociente de números no negativos es el cociente de las raíces cuadradas de dichos números:
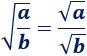
Ejemplo
Raíz cuadrada de la fracción 16/4:
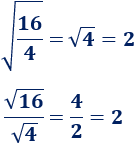
3. Cuadrado de una raíz
El cuadrado de la raíz cuadrada de un número no negativo es dicho número:
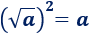
Ejemplos
- Cuadrado de la raíz cuadrada de 2:
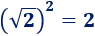
- Cuadrado de la raíz cuadrada de 3:
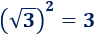
Esta propiedad es fácil de entender aplicando la propiedad del producto de raíces y la definición de raíz cuadrada:
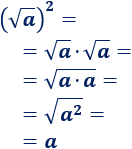
Ejemplo
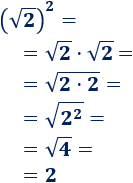
4. Raíz de un cuadrado
La raíz cuadrada del cuadrado de un número no negativo es dicho número:
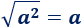
Ejemplos
- La raíz cuadrada del cuadrado de 2 es 2:
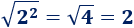
- La raíz cuadrada del cuadrado de 3 es 3:
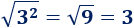
Esta propiedad es una consecuencia directa de la definición porque la raíz cuadrada de \(a^2\) es el número cuyo cuadrado es \(a^2\) y, lógicamente, dicho número es \(a\), ya que \(a^2 = a^2\).
Como consecuencia, podemos introducir o extraer el cuadrado en/de la raíz cuadrada:
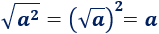
Nota: para aplicar esta propiedad cuando \(a\) sea negativo, tenemos que usar el valor absoluto:
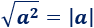
5. Problemas resueltos
Problema 1
Asociar, si es posible, los números de la columna izquierda con las raíces cuadradas de la columna derecha:
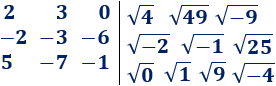
Solución:
Los números 2 y -2 son las raíces cuadradas de 4:
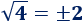
Los números 3 y -3 son las raíces cuadradas de 9:
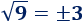
El número 0 es la raíz cuadrada de 0:
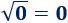
El número -1 es una raíz cuadrada de 1:
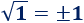
El número 5 es una raíz cuadrada de 25:
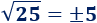
El número -7 es una raíz cuadrada de 49:
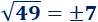
El único número de la columna izquierda que no se puede emparejar es -6, que es una raíz cuadrada de 36, la cual no aparece en la columna derecha:
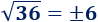
Las raíces de la columna derecha que no se pueden emparejar son las negativas: las raíces cuadradas de -1, -2, -4 y -9.
Problema 2
Comprobar que la raíz cuadrada de 6 entre la raíz cuadrada de 3 es igual a la raíz cuadrada de 2.
Solución:
Aplicamos la propiedad del cociente de raíces:
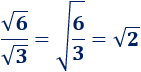
Problema 3
Si 4 tiene dos raíces cuadradas, ¿cuántas raíces tiene 64? ¿Y 0?
Solución:
En efecto, 4 tiene dos raíces cuadradas, que son 2 y -2:
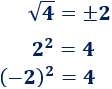
Lo mismo ocurre con todos los números positivos. Por ejemplo, las raíces cuadradas de 64 son 8 y -8:
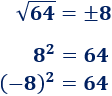
El 0 sólo tiene una raíz cuadrada porque no es negativo ni positivo. Además, su raíz cuadrada es 0:
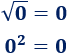
Problema 4
Calcular la raíz cuadrada de 144 sabiendo que este número se puede escribir como un producto de cuadrados:
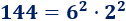
Solución:
Usaremos la propiedad de la raíz de un producto y de la raíz de un cuadrado:
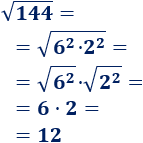
Por tanto, la raíz cuadrada de 144 es 12.
Problema 5 (para pensar)
Encontrar el error y explicar por qué está mal el siguiente razonamiento:
Como \(4 = (-2)^2\) y, además, \(a = \sqrt{a^2}\), entonces
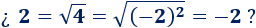
Solución:
Lógicamente, hay algo que está mal, puesto que 2 no es igual a -2.
Recordad que en las propiedades vistas anteriormente se dice siempre "número no negativo". Como -2 es negativo, no podemos aplicar las propiedades tal cual. De hecho, para que las propiedades sean ciertas para números positivos o negativos, debe usarse el valor absoluto. Por ejemplo,
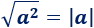
Modificamos el razonamiento anterior usando valor absoluto:
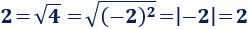
Problemas y Ecuaciones ©
ISSN 2659-9899