¿Cómo despejar en una fórmula?
En esta página explicamos qué es despejar o aislar una variable/incógnita en una fórmula y cómo hacerlo. Para ello, se utilizan ejemplos de fórmulas sencillas que se van complicando. Finalmente, proporcionamos algunos problemas resueltos de despejar en una fórmula.
Índice:
- ¿Qué es despejar o aislar?
- Fórmulas con una operación
- Fórmulas con dos operaciones
- Fórmulas con más de dos operaciones
- Problemas resueltos
1. ¿Qué es despejar o aislar?
Normalmente, las fórmulas están formadas por más de una variable o incógnita (letra) y en cada ocasión podemos necesitar una u otra de ellas.
Ejemplo
La fórmula de la distancia recorrida (\(d\)) por un móvil que se mueve a una velocidad constante (\(v\)) durante un tiempo (\(t\)) es la siguiente:
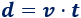
En esta fórmula podemos calcular la distancia (\(d\)) si conocemos la velocidad (\(v\)) y el tiempo (\(t\)), pero también podemos calcular la velocidad a partir de las otras dos variables (tiempo y distancia) mediante la fórmula
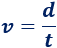
Esta segunda fórmula se ha obtenido de la anterior mediante el proceso que comúnmente se denomina "despejar" o "aislar" en la fórmula. En este caso se ha despejado la velocidad.
Despejar o aislar en una fórmula es una tarea básica, importante y sencilla, aunque debemos tener en cuenta varios aspectos para realizarla correctamente, los cuales vemos a continuación.
2. Fórmulas con una operación
La fórmula más sencilla es la que tiene una única operación.
Ejemplo 1: fórmula compuesta por una multiplicación

Los números y variables que multiplican en un lado pasan al otro lado dividiendo. Por tanto, es muy fácil despejar \(B\) y \(C\):
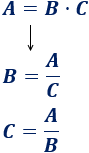
Ejemplo 2: fórmula compuesta por una división
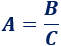
Los números y variables que dividen en un lado pasan al otro lado multiplicando. Por tanto, es muy fácil despejar \(B\):
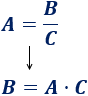
Para despejar \(C\) tenemos que hacer dos pasos:
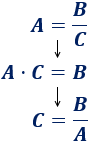
Hemos pasado la \(A\) dividiendo porque estaba multiplicando, como ya vimos anteriormente.
Ejemplo 3: fórmula compuesta por una suma
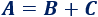
En este caso, como las variables \(B\) y \(C\) son los sumandos de una suma, pasan al otro lado restando:
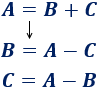
Ejemplo 4: fórmula compuesta por una resta
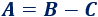
En este caso, hay que tener en cuenta que el signo del sumando \(B\) es positivo (no tiene signo delante) y el de \(C\) es negativo. Al igual que en las ecuaciones,
- Los sumandos que suman (signo +) pasan restando al otro lado.
- Los sumandos que restan (signo -) pasan sumando al otro lado.
Vamos a despejar \(B\) y \(C\) en la fórmula anterior \(A = B-C\):
- Despejamos la variable \(B\) de la fórmula pasando la \(C\) al otro lado:
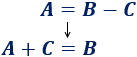
- Despejamos la variable \(C\) de la fórmula pasando la \(C\) al otro lado y la \(A\) al otro lado:
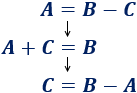
3. Fórmulas con dos operaciones
Cuando la fórmula tiene dos operaciones, es más complicado despejar: debemos saber cuál de las dos operaciones es la principal.
Ejemplo: fórmula con multiplicación como operación principal y suma como operación secundaria
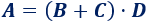
La operación principal de esta fórmula es la multiplicación, puesto que la suma es uno de los dos factores del producto.
Obtener la \(D\) es muy rápido porque forma parte de la operación principal. Como \((B+C)\)está multiplicando a \(C\), lo pasamos al otro lado dividiendo:
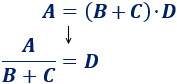
Para poder despejar la \(B\) o la \(C\), que están sumando, hay que "quitar" antes la \(D\), que forma parte de la operación principal.
La \(D\) pasa al otro lado dividiendo (porque está restando); la \(B\) y la \(C\) pasan al otro lado según si suman o restan.
- Despejamos la \(B\):
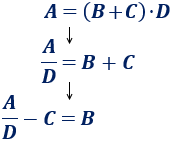
- Despejamos la \(C\):
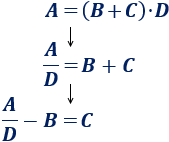
Observad que en las dos nuevas fórmulas obtenidas la operación principal es la resta.
4. Fórmulas con más de dos operaciones
Las fórmulas pueden tener más operaciones, en cuyo caso debemos operar de forma similar a los casos anteriores: teniendo en cuenta la operación principal. Además, pueden aparecer otro tipo de operaciones, por ejemplo, una potencia.
Ejemplo: fórmula con suma, producto y potencia
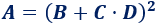
La operación principal es la potencia al cuadrado; después, la suma; y, después, la multiplicación.
Despejamos la \(C\) de la fórmula:
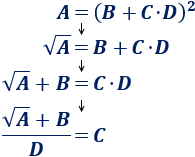
Nota: la potencia elevado a 2 se quita escribiendo la raíz cuadrada en el otro lado.
Importante: cuando pasamos una variable al otro lado, su operación afecta a todo el lado. En el ejemplo anterior, cuando pasamos la \(D\) dividiendo al otro lado, la \(D\) divide a TODO lo de la izquierda, es decir, a la suma.
5. Problemas resueltos
Problema 1
Despejar la \(C\) en la siguiente fórmula:
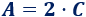
Solución:
Sólo tenemos que pasar el 2 dividiendo al otro lado:
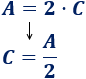
Problema 2
Despejar la \(C\) en la siguiente fórmula:

Solución:
Para obtener \(C\), primero tenemos que deshacer la resta, que es la operación principal:
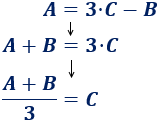
Problema 3
Despejar la \(C\) en la siguiente fórmula:
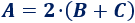
Solución:
Primero debemos quitar el 2 (dividiendo) y, después, la \(B\):
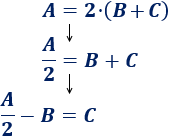
Problema 4
Despejar la \(C\) en la siguiente fórmula:
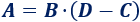
Solución:
Primero tenemos que quitar la \(B\) (dividiendo) y, después, la \(D\):
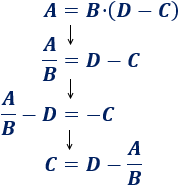
En el último paso hemos multiplicado los dos lados por -1 para que \(C\) sea positiva. Esto es lo mismo que cambiar todos los sumandos de un lado a otro.
Problema 5
Despejar la \(C\) en la siguiente fórmula:

Solución:
Primero, pasamos el 2 al otro lado restando (para deshacer la operación principal); después, pasamos la \(B\) dividiendo al otro lado:
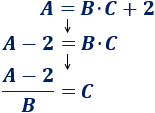
Problema 6 (difícil)
Despejar la \(C\) en la siguiente fórmula:

Solución:
En esta fórmula tenemos que ir realizando pasos hasta obtener al fin la \(C\):
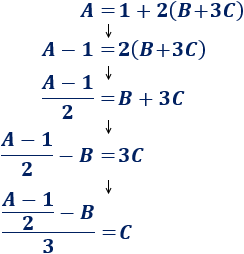
Teniendo en cuenta las propiedades de las fracciones, podemos reescribir la fórmula obtenida de forma más sencilla:
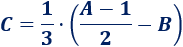
También,
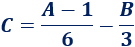
Otros temas relacionados:
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899