Proporcionalidad directa e inversa y regla de tres
Explicamos la relación de proporcionalidad simple directa e inversa y cómo aplicar una regla de tres, con ejemplos y problemas resueltos.
Índice:
- Ejemplos introductorios
- Proporcionalidad directa
- Proporcionalidad inversa
- Regla de tres
- Problemas resueltos
1. Ejemplos introductorios
Veamos un par de ejemplos con los que entenderemos fácilmente qué es una relación de proporcionalidad.
Proporcionalidad directa:
En una fábrica de balones, cada trabajador fabrica \(5\) balones al día. Si la empresa contrata más trabajadores, el número de balones que se fabrica será mayor.
Escribimos una tabla con el número de trabajadores y el de balones fabricados al día:
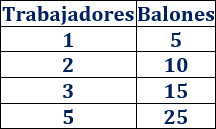
A medida que aumenta el número de trabajadores, lo hace el número de balones.
Estas dos magnitudes (número de trabajadores y de balones) mantienen una relación de proporcionalidad directa.
Si dividimos el número de balones entre el de trabajadores, obtenemos un resultado constante:
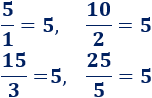
Este número se denomina constante de proporcionalidad o razón.
Proporcionalidad inversa:
El tiempo que se tarda en construir una casa entre \(2\) obreros es \(10\) meses. Si el número de obreros aumenta, el tiempo que se tarda es menor.
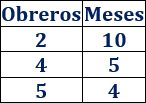
Estas dos magnitudes mantienen una relación de proporcionalidad inversa: cuando una magnitud aumenta, la otra disminuye y viceversa.
La constante de proporcionalidad se calcula multiplicando las magnitudes:
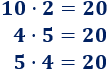
2. Proporcionalidad directa
Ya hemos visto que dos magnitudes son directamente proporcionales cuando
- Al aumentar una, también aumenta la otra.
- Al disminuir una, también disminuye la otra.
Las variaciones de las magnitudes deben producirse según la constante de proporcionalidad.
Ejemplo
Si en tres bolsas de naranjas caben \(36\) naranjas, ¿cuántas bolsas necesitamos para guardar \(48\) naranjas?
Solución:
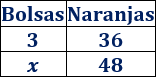
Como la proporcionalidad es directa (cuantas más naranjas, más bolsas), la constante de proporcionalidad es el cociente de las magnitudes:
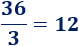
La constante de proporcionalidad debe ser la misma, así que
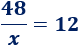
Despejando,
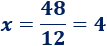
Necesitamos \(4\) bolsas.
3. Proporcionalidad inversa
Ya hemos visto que dos magnitudes son inversamente proporcionales cuando
- Al aumentar una, la otra disminuye.
- Al disminuir una, la otra aumenta.
Ejemplo
Si tardamos \(3\) minutos en recorrer una distancia a una velocidad de \(20 km/h\), ¿cuánto tardaremos en recorrer dicha distancia si circulamos a \(30 km/h\)?
Solución:
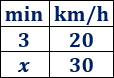
Como la proporcionalidad es inversa (cuanta más velocidad, menos tiempo), la constante de proporcionalidad es el producto de las magnitudes:

La constante de proporcionalidad debe ser la misma, así que

Despejando,
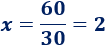
Tardaremos \(2\) minutos.
4. Regla de tres
Existe una regla que nos permite calcular una de las magnitudes a partir de la otra. Esta regla se denomina regla de tres (directa o inversa).
Proporcionalidad directa:
Nos ayudamos de un ejemplo.
Si en \(3\) horas llueven \(60\) litros de agua, ¿cuántos lloverán en \(5\) horas?
Escribimos los tres datos en una tabla, cada magnitud en su columna correspondiente:
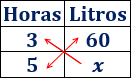
Observad las flechas representadas en forma de cruz. Los datos de la flecha doble se multiplican y el resultado se divide entre el dato de la flecha simple:
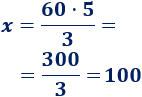
Lloverán \(100\) litros en \(5\) horas.
Proporcionalidad inversa:
Nos ayudamos de un ejemplo.
Si \(3\) trabajadores tardan \(2\) horas en cargar un camión, ¿cuánto tardarían en hacerlo \(4\) trabajadores?
Escribimos los tres datos en una tabla, cada magnitud en su columna correspondiente:
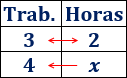
Observad las flechas paralelas. Los datos de la flecha doble se multiplican y el resultado se divide entre el dato de la flecha simple:
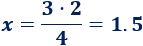
Dos obreros tardarían una hora y media.
5. Problemas resueltos
Problema 1
Determinar si las relaciones de proporcionalidad entre las siguientes magnitudes son directas o inversas:
- Tiempo necesario en recorrer una distancia y la velocidad a la que se circula.
- Tiempo necesario en recorrer una distancia y la distancia a recorrer.
- Tiempo necesario para llenar una piscina y el número de mangueras de agua que se emplean.
- Número de trabajadores y cantidad de trabajo realizado.
- Número de trabajadores que realizan una actividad en grupo y el tiempo necesario para realizar dicha actividad.
Solución:
- Inversa: a mayor velocidad, menos tiempo.
- Directa: a mayor distancia, más tiempo.
- Inversa: cuantas más mangueras, menos tiempo.
- Directa: cuantos más trabajadores, más trabajo se realiza.
- Inversa: cuantos más trabajadores, menos tiempo.
Problema 2
Un grupo de \(3\) alumnos tarda \(45\) minutos en hacer un proyecto de clase. ¿Cuánto se tardaría si el grupo es de \(5\) alumnos?
Solución:
Es una proporcionalidad inversa: cuantos más alumnos, menos tiempo tarda el grupo.
Aplicamos una regla de tres inversa:

El grupo tardaría \(27\) minutos.
Problema 3
Si el \(15\%\) de una cantidad es \(300\), ¿cuánto es el \(35\%\) de dicha cantidad?
Solución:
Los porcentajes son siempre relaciones de proporcionalidad directa.
Aplicamos una regla de tres directa:
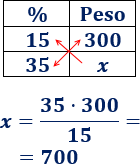
El \(35\%\) de dicha cantidad es \(700\).
Problema 4
En un examen de tipo test, Alberto obtuvo una nota de \(80\), lo que corresponde a \(120\) respuestas correctas. Si la nota de Leo fue \(66\), ¿cuántas respuestas correctas tuvo?
Solución:
Es una relación de proporcionalidad directa: cuanta más nota, más respuestas correctas.
Aplicamos una regla de tres directa:

Leo tuvo \(99\) respuestas correctas.
Problema 5
Leo y Alberto tardan \(15\) horas en pintar la casa de Leo. ¿Cuánto tardarían en pintarla si Teresa les ayuda?
Solución:
Es una proporcionalidad inversa: cuanta más gente, menos tiempo.
Aplicamos una regla de tres inversa:
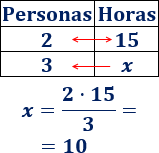
Entre los tres, tardarían \(10\) horas.
Más problemas similares: proporcionalidad simple y proporcionalidad compuesta.