Intersección de rectas y parábolas
Explicamos cómo calcular la intersección de rectas y parábolas entre sí, con ejemplos y problemas resueltos.
Índice:
- Recta y parábola (recordatorio)
- Intersección
- Problemas resueltos
1. Recta y parábola
Recordamos la ecuación de una recta:

El coeficiente \(m\) es la pendiente y \(n\) es la ordenada en el origen.
La ecuación de una parábola es
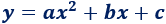
Ejemplo
Un ejemplo de recta es \(y = 2x-1\):
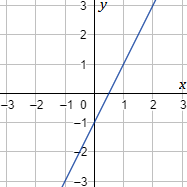
Un ejemplo de parábola es \( y = 2x²-1\):
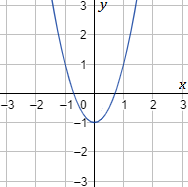
2. Intersección
La intersección de dos rectas es el punto donde éstas se cortan. Se calcula igualando sus ecuaciones. Al resolver la ecuación resultante, se obtienen las coordenadas del punto de corte.
Las rectas paralelas (las que tienen la misma pendiente, como \(y = 2x+1\) e \(y = 2x-3\)) no se cortan (no hay intersección).
Ejemplo 1
Intersección de dos rectas
Sean las rectas
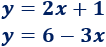
Igualamos las ecuaciones de las rectas:
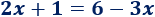
Resolvemos la ecuación obtenida:
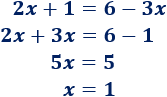
Como tenemos \(x\), sustituimos en cualquiera de las ecuaciones para obtener \(y\):
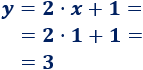
Por tanto, las dos rectas se cortan en el punto \((1,3)\).
Representación:
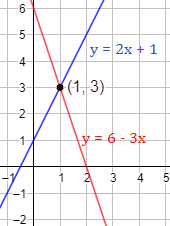
Ejemplo 2
Intersección de una recta y una parábola
Calculamos la intersección de la siguiente parábola y recta:
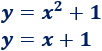
Igualamos las ecuaciones:
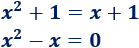
Resolvemos la ecuación de segundo grado incompleta:
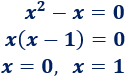
Hay dos soluciones: \(x=0\) y \(x=1\).
Calculamos \(y\) (usando los dos valores que tenemos para \(x\)):
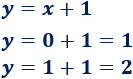
Por tanto, hay dos puntos de corte:
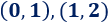
Representación:
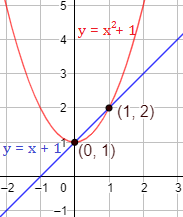
Ejemplo 3
Intersección de dos parábolas
Calculamos la intersección de las siguientes parábolas:
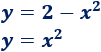
Igualamos las ecuaciones:
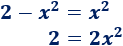
Resolvemos la ecuación de segundo grado incompleta:
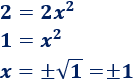
Calculamos \(y\):
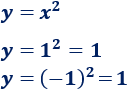
Por tanto, hay dos puntos de corte:
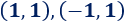
Representación:
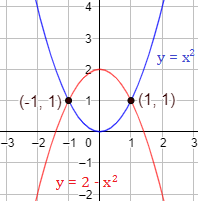
4. Problemas resueltos
Problema 1
Hallar el punto de corte (o intersección) entre las siguientes rectas:
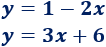
Solución:
Sólo tenemos que igualar ambas ecuaciones:
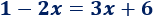
Resolvemos la ecuación:
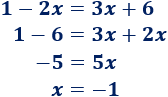
Calculamos la otra coordenada:
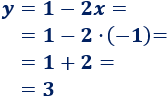
El punto de intersección de las rectas es
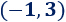
Representación:
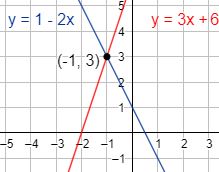
Problema 2
Hallar el punto de corte entre las siguientes parábola y recta:
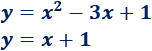
Solución:
Igualamos ambas ecuaciones:
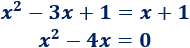
Resolvemos la ecuación cuadrática incompleta:
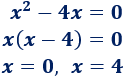
Como hay dos soluciones, hay dos puntos de intersección.
Calculamos la otra coordenada:
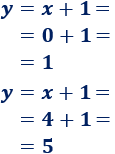
Por tanto, los dos puntos de intersección son
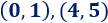
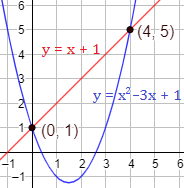
Representación:
Problema 3
Hallar la intersección entre las siguientes parábola y recta:
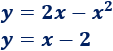
Solución:
Igualamos las ecuaciones:
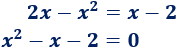
Resolvemos la ecuación cuadrática completa:
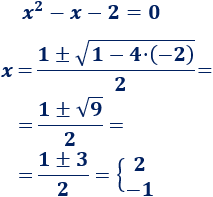
Calculamos la otra coordenada:
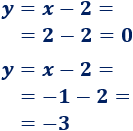
Por tanto, los dos puntos de intersección son
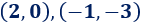
Representación:
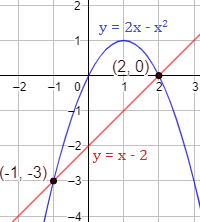
Problema 4
Hallar la intersección entre las siguientes parábolas:
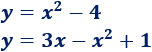
Solución:
Igualamos las ecuaciones:
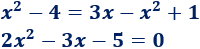
Resolvemos la ecuación cuadrática completa:
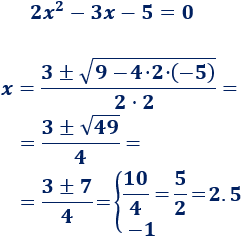
Calculamos la segunda coordenada:
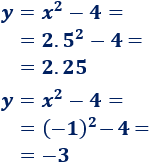
Los puntos de intersección son
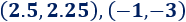
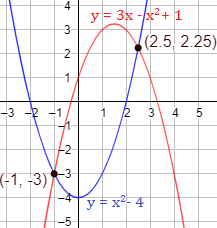
Representación:
Más problemas similares: rectas y parábolas.