¿Qué es una función inyectiva?
En esta página explicamos el concepto de inyectividad de una función y proporcionamos algunos ejemplos de funciones inyectivas y no inyectivas y problemas relacionados resueltos.
Índice:
- Concepto intuitivo de inyectividad
- Gráfica
- Demostrar la inyectividad
- Problemas para pensar
1. Concepto intuitivo de inyectividad
Disponemos de dos definiciones equivalentes:
- Una función es inyectiva cuando dados \(a\neq b\), entonces \(f(a) \neq f(b)\), es decir,
-
Si dos números del dominio son distintos, entonces sus imágenes son distintas.
- Una función es inyectiva si cuando \(f(a) = f(b)\), entonces \(a = b\), es decir,
-
Si las imágenes de dos números son iguales, entonces dichos números son iguales.
Ejemplos
- La función \(f(x) = x^2\) no es inyectiva ya que \(f(-2) = 4 = f(2)\). Gráfica:
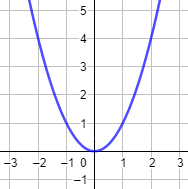
- La función \(f(x) = x\) es inyectiva porque \(f(a) = f(b)\) si, y sólo si, \(a = b\). Gráfica:
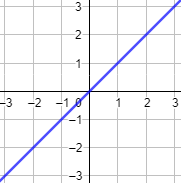
- La función \(f(x) = |x|\) no es inyectiva, puesto que \(f(x) = f(-x)\). Gráfica:
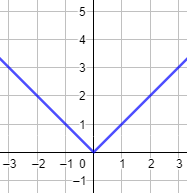
- La función constante \(f(x) = 3\) no es inyectiva. Gráfica:
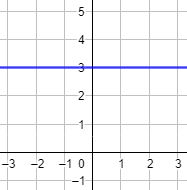
2. Gráfica
Detectar los puntos \(a \neq b\) para los cuales \(f(a) = f(b)\) (y, por tanto, hacen que la función no sea inyectiva) es sencillo observando la gráfica: si imaginamos rectas horizontales, dichos puntos son aquellos en los que la recta tiene más de una intersección con la gráfica de la función.
Ejemplo
Gráfica de la función \(f(x) = x^3 - x \) (en azul):
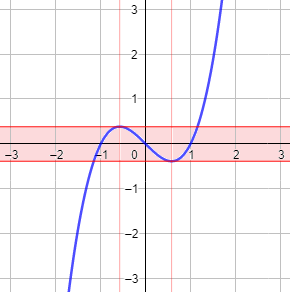
En la banda de color rojo se encuentran los puntos donde falla la inyectividad de esta función, que son, en concreto,
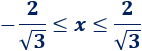
Por ejemplo, \(x = -1\), \(x=0\) y \(x=1\) son tres números distintos de dicho intervalo que comparten imagen:
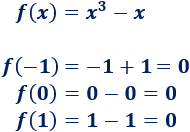
3. Demostrar la inyectividad
Para demostrar que una función es inyectiva, probamos que si \(f(a) = f(b)\), entonces \(a = b\) (esto es lo mismo que demostrar que si \(a\neq b\), entonces \(f(a) \neq f(b)\)).
Ejemplo 1
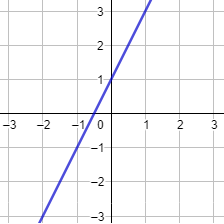
Demostramos que la función \(f(x) = 2x+1\) es inyectiva.
Suponiendo \(f(a) = f(b)\), obtenemos \(a=b\):
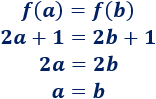
Gráfica:
Ejemplo 2
Demostramos que \(f(x) = x^4-2x^2\) no es inyectiva.
Tenemos que ver que si \(f(a) = f(b)\), no necesariamente \(a = b\):
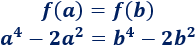
Como tenemos exponentes pares, podemos usar números negativos.
Sean \(a> 0\) y \(b = -a\), entonces
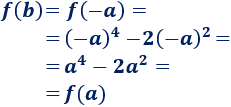
Es decir, tenemos
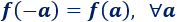
Esto significa que la gráfica de la función es simétrica respecto del eje de ordenadas.
Además, si \(a=0\),
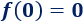
Y \(0\) no es sólo imagen de \(a = 0\), puesto que \(0 = x^4-2x^2\) tiene tres raíces distintas: \(x = 0\) y \(x = \pm \sqrt{2}\), así que
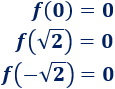
Gráfica:
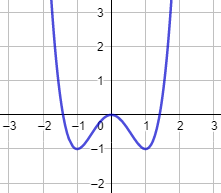
4. Problemas para pensar
Problema 1
Si una función es estrictamente creciente, ¿es inyectiva?
Solución:
Sí.
La definición de función estrictamente creciente es
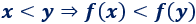
La inyectividad es inmediata, puesto que, si dos números son distintos, entonces uno es mayor que el otro y, por tanto, lo mismo ocurre con sus imágenes.
Como consecuencia, las rectas no horizontales (ni verticales) son funciones inyectivas.
Problema 2
Sea \(y = f(x)\) una función que tiene dos raíces distintas. ¿Es una función inyectiva?
Solución:
No.
Sean \(a\) y \(b\) las raíces, entonces
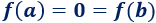
La función no es inyectiva porque \(f(a) = f(b)\) pero \(a \neq b\).
Problema 3
Sea la función \(f(x) = x^q\), siendo \(q\) un número natural par. ¿Es una función inyectiva?
Solución:
No.
Si \(q\) es un número par, entonces la función no puede ser inyectiva, ya que \(f(a) = f(-a)\).
Problema 4
Sea la función \(f(x) = x^q\), siendo \(q\) un número natural impar. ¿Es una función inyectiva?
Solución:
Sí.
Si \(q\) es un número impar, entonces \(f(x) = x^q\) es una función estrictamente creciente, con lo que es inyectiva.
Otros temas relacionados:
- Función inversa
- Función sobreyectiva
- Dominio y recorrido de una función
- ¿Qué es una ecuación?
- ¿Todas las ecuaciones tienen solución?
- ¿Cuántas soluciones tiene una ecuación?
- ¿Hay ecuaciones sin solución?
- ¿Por qué se dice al cuadrado y al cubo?
- Pasar de un lado a otro de la igualdad
Problemas y Ecuaciones ©
ISSN 2659-9899