Problemas de movimiento rectilíneo uniforme (MRU)
En esta página vamos a resolver 15 problemas de movimiento rectilíneo uniforme (MRU), es decir, problemas de móviles que se mueven en línea recta y a velocidad constante.
La fórmula del MRU es
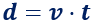
siendo
- \(d\) la distancia recorrida,
- \(v\) la velocidad del móvil y
- \(t\) el tiempo que dura el movimiento
Para calcular la velocidad o el tiempo, despejamos en la ecuación anterior:
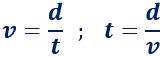
Trucos y consejos
- Para recordar las fórmulas, os puede ayudar lo siguiente: como a todos nos suena la velocidad en km/h, la velocidad es la distancia dividido entre el tiempo (km/h): v = d/t. Las otras fórmulas las calculamos despejando: lo que multiplica pasa al otro lado dividiendo y viceversa.
- Comprobad que las variables del movimiento (\(v\), \(d\) y \(t\)) tengan las mismas unidades de medida.
- Escribid las unidades de medida de las variables en las operaciones.
Problemas resueltos
Problema 1 

¿A qué velocidad debe circular un auto de carreras para recorrer 50km en un cuarto de hora? ¿Y si quiere recorrerlos en solo 9 minutos?
Resolvemos:
Como la distancia es en kilómetros, vamos a escribir el tiempo en unidades de hora para tener la velocidad en km/h.
El tiempo que dura el movimiento es un cuarto de hora, lo que equivale a 0.25 horas:

Observad que en la operación anterior se cancelan los "min" porque aparecen en el numerador y en el denominador, quedando las horas, que es la unidad que queremos (esto nos asegura que hemos hecho el cambio correctamente).
La distancia recorrida por el móvil es de 50 km:

Aplicamos la fórmula del movimiento para calcular la velocidad:
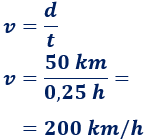
Por tanto, el auto debería circular a una velocidad de 200 km/h.
Ahora, supongamos que el tiempo es \(t = 9\text{ min}\).
Pasamos de minutos a horas:

Aplicamos la fórmula:
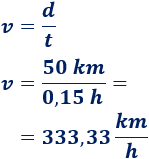
Entonces, debería circular a 333,33 km/h.
Tabla resumen:

Nota: observad que al escribir las unidades de medida en las operaciones, obtenemos las unidades de medida correspondientes del resultado. Esto nos permite evitar posibles errores.
Problema 2 
Una bicicleta circula en línea recta a una velocidad de 15km/h durante 45 minutos. ¿Qué distancia recorre? ¿Y si circulara a 20km/h?
Resolvemos:
La velocidad de la bicicleta es
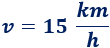
El tiempo que dura el movimiento es 45 minutos. Como las unidades de velocidad son kilómetros por hora y el tiempo está en minutos, tenemos que pasar el tiempo de minutos a horas (dividiendo entre 60):
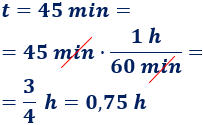
Este paso es esencial porque no obtendremos el mismo resultado si escribimos \(t = 45\) que \(t = 0,75\).
Calculamos la distancia que recorre la bicicleta mediante la fórmula del movimiento:

Calculamos la distancia que recorrería si circula a 20km/h en lugar de a 15km/h:
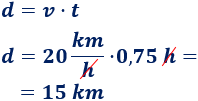
Por tanto, si circula durante 45 minutos a 15km/h, recorrería 11,25km; mientras que si circula a 20km/h, recorrería 15km.
Problema 3 
Si Alberto recorre con su patinete una pista de 300 metros en un minuto, ¿a qué velocidad circula? ¿Y si reduce el tiempo a 40 segundos?
Expresar la velocidad en m/s y en km/h.
Resolvemos:
La distancia que recorre durante el movimiento es de 300 metros:

Y el tiempo es 1 minuto, pero nos interesa en segundos:

Calculamos la velocidad a la que circula Alberto es
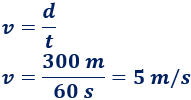
Calculamos la velocidad si reduce el tiempo a 40 segundos:
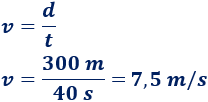
Ahora, escribimos ambas velocidades en km/h:

Nota: observad cómo escribir las unidades de medida nos facilita realizar las operaciones.
Problema 4 

¿Cuántos metros recorre una motocicleta en un segundo si circula a una velocidad de 90km/h? ¿Y si circula a 270 km/h?
Resolvemos:
Como tenemos la velocidad en km/h, la pasamos a metros por segundo:

Como la velocidad de la motocicleta es 25 m/s, recorre 25 metros en un segundo.
En cambio, si la velocidad es de 270 km/h, entonces recorre 75 metros en un segundo porque

Observad que la segunda velocidad es el triple de la primera, así que, en el mismo tiempo (1 segundo), recorre el triple de metros.
Problema 5 (a) 
¿A qué velocidad circula el móvil cuya gráfica de velocidad en función del tiempo es la siguiente?
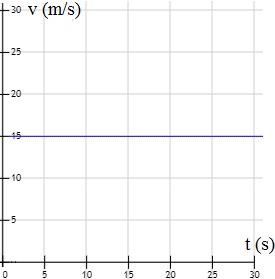
- ¿Qué distancia recorre el móvil si el movimiento dura 1 minuto con la misma velocidad?
- ¿Tendría el mismo aspecto la gráfica de la distancia recorrida en función del tiempo?
Resolvemos:
La gráfica nos indica la velocidad del móvil en cada instante. Como se trata de una gráfica horizontal, la velocidad se mantiene constante durante los 30 segundos y esta velocidad es de 15 metros por segundo:

Si el movimiento dura 1 minuto, es decir, 60 segundos, la distancia que recorre es 900 metros:
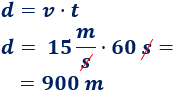
La gráfica de la distancia recorrida en función del tiempo sería una recta creciente ya que la distancia aumenta a medida que pasa el tiempo y, además, lo hace de forma lineal por ser la velocidad constante: \(d = 15\cdot t\).
Problema 5 (b) 
¿Cuál es la velocidad de un móvil que circula en línea recta y cuya gráfica de distancia recorrida en función del tiempo es la siguiente?
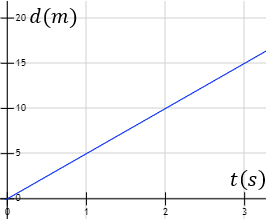
Observando la gráfica, ¿qué distancia habrá recorrido el móvil en 3 segundos?
Resolvemos:
La gráfica es una recta creciente, lo que significa que la distancia aumenta de forma lineal en función del tiempo, lo cual se corresponde a un MRU.
Observando la gráfica, vemos que la recta pasa por los puntos (1, 5) y (2, 10), por lo que podemos asegurar que se trata de la gráfica de la función
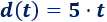
Comprobamos que los puntos están en la gráfica:
- Si \(t = 1\), entonces \( d(1) = 5\).
- Si \(t = 2\), entonces \(d(2) = 5\cdot 2 = 10\).
- Si \(t = 3\), entonces \(d(3) = 5\cdot 3 = 15\).
Finalmente, observamos que la función es como la fórmula del MRU: \(d = v\cdot t\), lo que quiere decir que la velocidad del móvil es \(v = 5\ m/s\) (la distancia es en metros y el tiempo en segundos).
Observamos la gráfica: cuando \(t = 3s\), entonces \(d = 15m\), lo que quiere decir que el móvil ha recorrido 15 metros en 3 segundos.
Problema 6 
Un objeto del espacio se mueve en línea recta con velocidad constante y la gráfica de su movimiento es la siguiente:
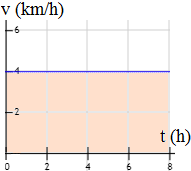
Responde:
- ¿cuál es su velocidad?
- ¿qué distancia recorre en 8 horas?
- ¿cuál es el área del rectángulo coloreado en naranja?
- ¿sabrías decir cuál es la relación del área coloreada con el movimiento?
Resolvemos:
La velocidad del objeto es v = 4 km/h.
Calculamos la distancia que recorre en t = 8 h:
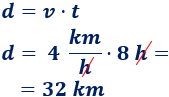
La base del rectángulo es 8 unidades y su altura es 4 unidades. Por tanto, su área es 8·4 = 32 unidades al cuadrado.
Si utilizamos las unidades de los ejes (h y km/h), el área coincide con la distancia que recorre el objeto:
- la base es el tiempo \(t\)
- la altura es la velocidad \(v\)
- el área es \(v\cdot t = d\), es decir, la distancia recorrida \(d\).
Problema 7 
-
¿La siguiente gráfica puede ser la gráfica de un movimiento rectilíneo uniforme? ¿Por qué?
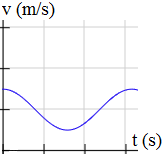
-
¿La siguiente gráfica puede ser la gráfica de un movimiento rectilíneo uniforme? ¿Por qué?
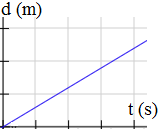
Resolvemos:
La primera gráfica no puede ser la gráfica de un MRU porque la velocidad en un MRU es constante y, por tanto, su gráfica de la velocidad en función del tiempo debe ser una recta horizontal. La velocidad representada en la gráfica decrece y crece.
La segunda gráfica sí puede ser la gráfica de un MRU porque en un MRU la distancia recorrida crece de forma uniforme. La gráfica de la distancia recorrida en función del tiempo debe ser una recta diagonal creciente (una recta lineal creciente).
Problema 8 
- Si un avión tarda 2 segundos en recorrer 160 metros, ¿cuál es su velocidad en km/h?
- ¿Cuánto tardaría en volar desde Buenos Aires a Madrid un avión que vuela a 900km/h? La distancia entre estas ciudades es de unos 10 mil kilómetros.
Resolvemos:
Calculamos la velocidad:
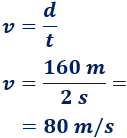
Pasamos la velocidad a kilómetros por hora:

Calculamos cuánto tardaría un avión en recorrer 10 mil kilómetros a una velocidad de 900km/h:
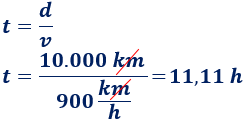
Escribimos las 0,11 horas en minutos:
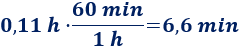
El avión tardaría unas 11 horas y 6 minutos y medio.
Problema 9 
Sabiendo que la velocidad del sonido es de 343,2 m/s, ¿a cuántos kilómetros de distancia se produce un trueno que tarda 6 segundos en oírse? ¿Cuánto tardaría en oirse un trueno si tiene lugar a 10 km de distancia?
Resolvemos:
Calculamos la distancia:
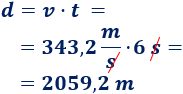
Pasamos la distancia a kilómetros:

Calculamos el tiempo si la distancia es 10 km:
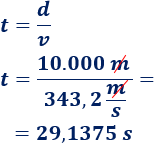
Problema 10 
La velocidad de la luz en el vacío es, aproximadamente, c = 300.000 km/s.
- ¿Cuánto tarda en llegar la luz del Sol al planeta Tierra si éstos distan unos 149,6 millones de kilómetros?
- ¿Y en llegar a Júpiter, situado a unos 748 millones del Sol?
- Si la circunferencia alrededor del ecuador de la Tierra es de unos 40 mil km, ¿cuántas vueltas le daría la luz solar en 1 segundo?
Resolvemos:
La fórmula para calcular el tiempo es \(t = d/v\).
Sustituimos los datos:

Por tanto, la luz del Sol tarda unos 8,31 minutos en llegar a la Tierra.
Calculamos cuánto tarda en llegar a Júpiter:

Como sabemos que la luz recorre unos 300 mil km en 1 segundo, para calcular el número de vueltas en 1 segundo solo tenemos que dividir 300 mil entre 40 mil:

Problema 11 
Javier necesita ir con urgencia al kiosco a comprar el último número de su revista preferida, por lo que debe decidir entre:
- acudir al kiosco A, situado en una calle peatonal, caminando una distancia de 300 metros a una velocidad de 4,5 km/h,
- o bien, acudir al kiosco B, pedaleando en su bicicleta durante 1 kilómetro a una velocidad de 15 km/h.
¿Qué opción le conviene más?
Resolvemos:
La velocidad de la segunda opción es mayor, pero la distancia a recorrer también es mayor. Debemos calcular el tiempo de los dos movimientos para poder comparar.
Primer movimiento
- Distancia: 300 m = 0,3 km
- Velocidad: 4,5 km/h
Calculamos el tiempo:

Segundo movimiento
- Distancia: 1 km
- Velocidad: 15 km/h
Calculamos el tiempo:
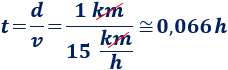
Javier tardaría exactamente lo mismo en ambas opciones: 0,066 horas, es decir, 4 minutos.
Problema 12 
Los puntos A y B del mapa se encuentran situados a 100km de distancia en línea recta. En el mismo instante
- parte una moto del punto A hacia el punto B a una velocidad de 110 km/h,
- parte un camión del punto B hacia el punto A a una velocidad de 80 km/h.
Calcular cuánto tardarán en encontrarse ambos vehículos que circulan por la misma carretera, pero en sentido contrario.
Resolvemos:
Representación del problema:
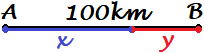
Debemos considerar dos movimientos distintos: el de la moto y el del camión.
Como los movimientos comienzan en el mismo instante, cuando se encuentren, habrá transcurrido el mismo tiempo para ambos. Es decir, el tiempo \(t\) será el mismo.
Cuando se encuentren los vehículos, la moto habrá recorrido una distancia \(x\) y el camión, \(y\). Como la distancia entre los puntos de partida es de 100 km, entonces tenemos la ecuación
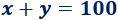
Calculamos el tiempo de la moto (velocidad 110 km/h y distancia \(x\)):
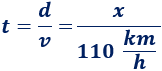
Calculamos el tiempo del camión (velocidad 80km/h y distancia \(y\)):
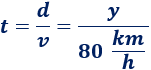
Como los tiempos son iguales, podemos igualarlos (\(t = t\)) y obtenemos
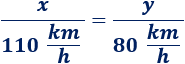
Podemos eliminar las unidades de la velocidad para ver con mayor claridad la ecuación:
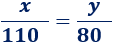
Pasamos los denominadores al otro lado y aislamos la incógnita \(x\):
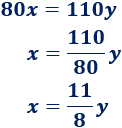
Sustituimos en la primera ecuación del problema:
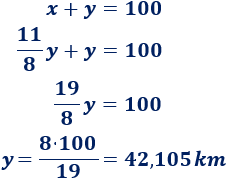
Cuando los vehículos se encuentren, el camión habrá recorrido 42,105 kilómetros. Podemos calcular el tiempo a partir de la fórmula de su movimiento:
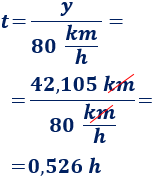
Por tanto, el tiempo que tardan en encontrarse es 0,526 horas, es decir, unos 31,5 minutos.
Problema 13 
Completar la siguiente tabla que proporciona los datos de los movimientos independientes de 5 móviles mediante la fórmula del movimiento \(d = v\cdot t\):

¿Cuál es móvil que tiene una mayor velocidad?
Resolvemos:
Móvil 1
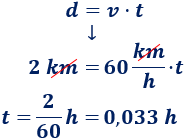
Móvil 2
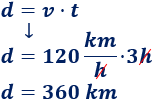
Móvil 3
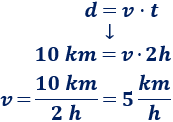
Móvil 4
Tenemos la velocidad en m/s y el tiempo en minutos.
Como después tenemos que comparar las velocidades, la escribimos en km/h:

Y el tiempo, por tanto, en horas:

Aplicamos la fórmula para calcular la distancia:
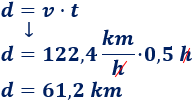
Móvil 5
Pasamos el tiempo a horas:
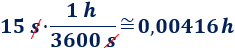
Aplicamos la fórmula:
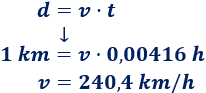
Nota: si usamos el tiempo exacto (sin aproximar), 1/240 horas, la velocidad es 240 km/h.
Completamos la tabla:
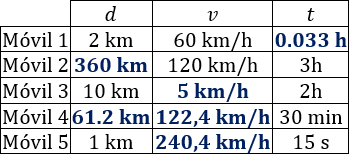
Observando la tabla, el móvil que tiene una velocidad mayor es el móvil 5.
Problema 14 
Una nave espacial se mueve en línea recta a una velocidad de 8000 km/h durante 15 minutos. Entonces, acelera drásticamente (instantemente) hasta una velocidad de 12000 km/h y mantiene dicha velocidad durante 15 minutos más.
¿Cuál es la distancia que ha recorrido durante los 30 minutos del trayecto?
Resolvemos:
Es importante señalar que el cambio de velocidad se produce de forma instantánea para poder considerar el movimiento como dos movimientos MRU seguidos y NO un movimiento acelerado.
Calculamos la distancia recorrida en los primeros 15 minutos (0,25 h):
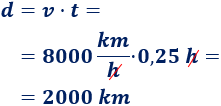
Calculamos la distancia recorrida en los siguientes 15 minutos (0,25 h):
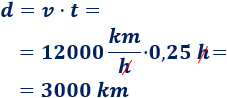
En los 30 minutos la nave habrá recorrido 5 mil kilómetros.
Problema 15 
La galaxia enana de Can Mayor es la galaxia más cercana a la Vía Láctea situada a unos 25 mil años luz del sistema solar.
Un año luz es la distancia que la luz tarda un año (365,25 días) en recorrer.
Aproximando la velocidad de la luz a 300 mil kilómetros por segundo, ¿a cuántos kilómetros se encuentra la galaxia de Can Mayor del sistema solar?
¿Cuánto tardaría en viajar una nave espacial desde el sistema solar a dicha galaxia si se mueve a la velocidad de la luz?
Resolvemos:
Solo tenemos que pasar los 25 mil años luz a kilómetros.
Primero, calculamos cuántos kilómetros recorre la luz en 1 año (365,25 días) y, después, multiplicamos el resultado por 25 mil.
Calculamos cuántos segundos hay en un año:
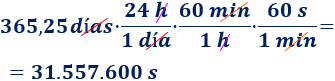
Como la luz recorre unos 300 mil kilómetros en un segundo, entonces en un año recorre

Multiplicamos por 25 mil, es decir, por \(25\cdot 10^3\):
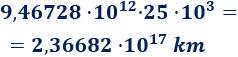
En notación decimal, la galaxia enana de Can Mayor se encuentra a unos 236.682.000.000.000.000 km.
Como la galaxia se encuentra a 25 mil años luz, una nave que viaje a la velocidad de la luz tardaría 25 mil años en realizar el trayecto.
Más problemas similares: Problemas de movimiento rectilíneo uniforme.