Teorema de Pitágoras
En esta página resolvemos problemas aplicando el Teorema de Pitágoras. Este teorema establece que la suma de los cuadrados de los catetos de un triángulo rectángulo es igual al cuadrado de la hipotenusa:
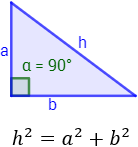
Recordad que un triángulo es rectángulo cuando uno de sus ángulos interiores es recto (90 grados) y que la hipotenusa es el lado opuesto al ángulo recto.
Enlace: Calculadora de Pitágoras.
Problema 1 
En el siguiente triángulo, ¿cuál de los lados es la hipotenusa y cuál es el ángulo recto?
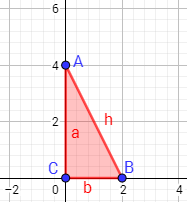
Calcular cuánto mide la hipotenusa.
Resolvemos:
Los catetos son los lados \(a\) y \(b\). La hipotenusa es el lado \(h\). El ángulo recto es el ángulo que forman ambos catetos.
Para calcular la longitud de la hipotenusa, aplicamos Pitágoras. Los catetos miden \(a = 2\) y \(b = 4\), con lo que
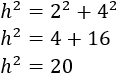
Finalmente, hacemos la raíz cuadrada:
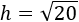
Simplificamos el resultado escribiendo el radicando como un producto y aplicando la propiedad de que la raíz de una producto es el producto de las raíces de sus factores:
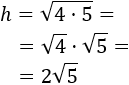
Si aproximamos, \( h \simeq 4,47\).
Problema 2 
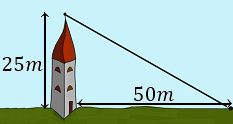
Se quiere colocar un cable desde la cima de una torre de 25 metros altura hasta un punto situado a 50 metros de la base la torre. ¿Cuánto debe medir el cable?
Resolvemos:
El cable coincide con la hipotenusa de un triángulo rectángulo cuyos catetos miden \(a = 25m\) y \(b = 50m\).
Calculamos la longitud del cable (es la hipotenusa \(h\)):
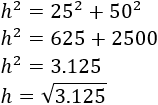
Como \(3.125 = 25^2\cdot 5\), podemos simplificar:
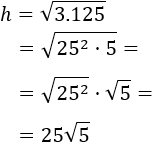
El cable debe medir \(h = 25\sqrt{5}\) metros, es decir, aproximadamente 55.9 metros.
Problema 3 
Una parcela de terreno cuadrado dispone de un camino de longitud \(2\sqrt{2}\) kilómetros (segmento discontinuo) que la atraviesa según se muestra en la siguiente imagen:
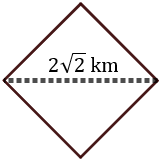
Calcular el área total de la parcela.
Resolvemos:
Observando la figura, el camino coincide con una de las diagonales del cuadrado, así que divide a éste en dos triángulos iguales. Además, los dos triángulos son rectángulos y los catetos miden lo mismo.
Si llamamos \(x\) a la medida de los catetos, aplicando Pitágoras,
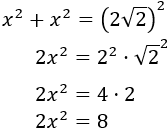
Hemos usado que el cuadrado de un producto es el producto de los cuadrados.
Para calcular \(x\), pasamos el 2 dividiendo al otro lado de la igualdad y hacemos la raíz cuadrada:
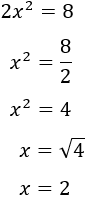
Por tanto, los cuatro lados de la parcela miden 2 kilómetros y, por consiguiente, su área es 4 kilómetros cuadrados.
Problema 4 
La hipotenusa de un triángulo rectángulo mide 10 metros y sus catetos miden \(x\) y \(x+2\):
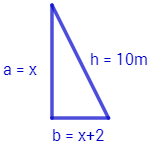
¿Cuánto miden los catetos?
Resolvemos:
Por Pitágoras, \(h^2 = a^2 + b^2\), con lo que
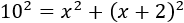
No olvidemos la fórmula del cuadrado de un binomio:
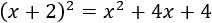
Sustituyendo,
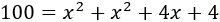
Simplificamos la ecuación:
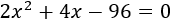
Resolvemos la ecuación de segundo grado:
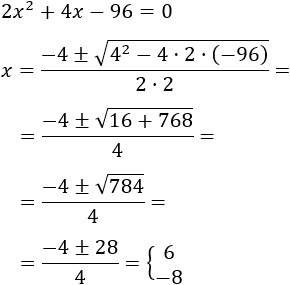
Como \(x\) representa una longitud, la solución debe ser positiva: \(x = 6\). Los catetos miden 6 y 8 metros.
Problema 5 
Se desea pintar una cuadrado inscrito en una circunferencia de radio \(R = 3cm\) como se muestra en la figura:
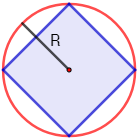
Calcular el área del cuadrado.
Resolvemos:
El radio mide \(R = 3cm\). El diámetro (\( d=2R\)) coincide con la diagonal del cuadrado y, por ende, divide al cuadrado en dos triángulos rectángulos iguales:
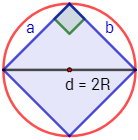
Como la figura es un cuadrado, los catetos \(a\) y \(b\) miden lo mismo, así que escribiremos simplemente \(a\). La hipotenusa mide dos veces el radio: \(h = 2\cdot 3 =6cm\).
Aplicamos el teorema de Pitágoras para calcular los lados del cuadrado:
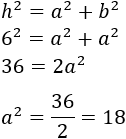
No calculamos la raíz cuadrada ya que no necesitamos saber cuánto miden los lados del cuadrado.
El área de un cuadrado de lado \(a\) es \(a^2\). Por tanto, el área del cuadrado inscrito es 18 centímetros cuadrados.
Problema 6 
Calcular cuánto mide el cateto \(b\) de un triángulo rectángulo si su otro cateto, \(a\), y su hipotenusa, \(h\), miden
$$ a = \frac{3\sqrt{2}}{2} m $$
$$ h = \frac{\sqrt{194}}{6} m $$
Resolvemos:
Por Pitágoras, sustituyendo \(a\) y \(h\),
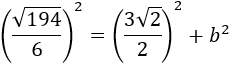
Aplicamos las propiedades de las potencias para calcular los cuadrados:
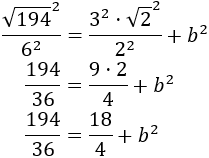
Calculamos \(b\):
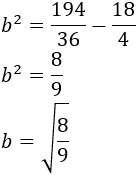
Aplicamos las propiedades de las raíces para simplificar:
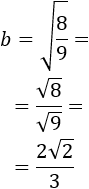
Por tanto, el cateto \(b\) mide \(\frac{2\sqrt{2}}{3} m\).
Problema 7 
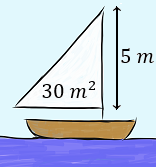
Hallar las medidas de los lados de una vela con forma de triángulo rectángulo si se quiere que tenga un área de 30 metros al cuadrado y que uno de sus catetos mida 5 metros para que se pueda colocar en el mástil.
Resolvemos:
Llamamos \(a\), \(b\) y \(h\) a la altura, base e hipotenusa de la vela.
Por un lado, como el área de un triángulo es base por altura, tenemos
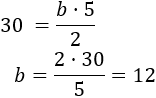
De donde tenemos que la base debe medir 12 metros.
Por otro lado, como la vela tiene forma de triángulo rectángulo, podemos calcular la hipotenusa por Pitágoras:
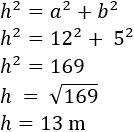
Por tanto, los lados de la vela deben medir 5, 12 y 13 metros.
Problema 8 
Si el cateto de un triángulo rectángulo mide \(x\) y el otro mide el doble, obtener una fórmula para calcular la longitud de la hipotenusa en función del cateto menor, \(x\).
Utilizar la fórmula obtenida para calcular la hipotenusa cuando \(x = \sqrt{5}\) y \(x = 2\cdot \sqrt{5}\).
Resolvemos:
Supongamos que uno de los catetos mide \(x\), entonces el otro debe medir \(2x\). Para calcular la hipotenusa, \(h\), aplicamos Pitágoras:
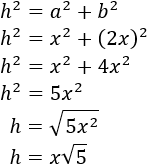
Aplicamos la fórmula para \(x = \sqrt{5}\):
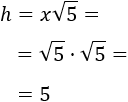
Aplicamos la fórmula para \(x = 2\cdot \sqrt{5}\):
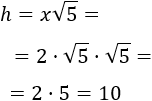
Problema 9 
Se tiene un rectángulo cuya base mide el doble que su altura y su área es 12 centímetros cuadrados. Calcular el perímetro del rectángulo y su diagonal.
Resolvemos:
Llamamos \(a\) y \(b\) a la altura y la base del rectángulo, respectivamente. Como la base es el doble que la altura, \(b = 2a\).
El área de un rectángulo es base por altura, así que
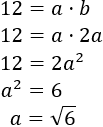
La altura del rectángulo mide \(\sqrt{6}cm\) y la base mide \(2\sqrt{6}cm\). El perímetro del rectángulo es \(6\sqrt{6}cm\).
Como la diagonal del rectángulo lo divide en dos triángulos rectángulos y sabemos cuánto miden los catetos, aplicamos Pitágoras para calcular la diagonal, \(d\):
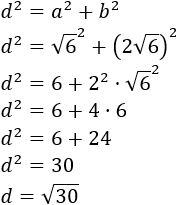
La diagonal del rectángulo mide \(\sqrt{30}\) centímetros.
Problema 10 
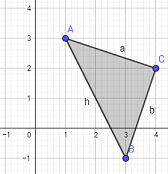
Calcular el área del triángulo rectángulo cuyos vértices son \(A = (1,3)\), \(B = (3,-1)\) y \(C=(4,2)\).
Resolvemos:
Observad la siguiente figura:
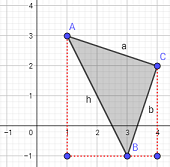
Podemos calcular el lado \(h\) y el lado \(b\) aplicando dos veces Pitágoras ayudándonos de los segmentos de color rojo, que forman triángulos rectángulos.
Los catetos del triángulo cuya hipotenusa es \(h\) miden 2 y 4 unidades. Por tanto,
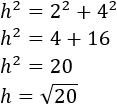
Los catetos del triángulo cuya hipotenusa es \(b\) miden 1 y 3 unidades. Por tanto,
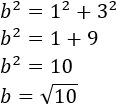
Conocemos la hipotenusa, \(h\), y la base, \(b\), del triángulo del problema. Aplicamos Pitágoras para calcular la altura \(a\):
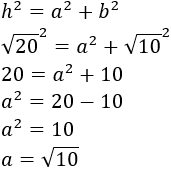
Calculamos el área del triángulo (base por altura entre 2):
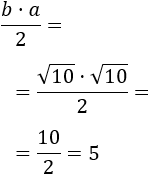
El área del triángulo es 5 unidades al cuadrado.
Más sobre Pitágoras: