Operaciones entre números complejos
En esta página vamos a explicar cómo sumar, restar, multiplicar y dividir números complejos.
Índice de contenidos:
- Sumar y restar en forma binómica
- Multiplicar y dividir en forma binómica
- Multiplicar y dividir en forma polar
Otros temas de números complejos:
- Introducción a los números complejos
- Módulo y argumento de un complejo
- Formas binómica, polar y trigonométrica
- Calculadora de operaciones entre complejos en forma binómica
1. Sumar y restar en forma binómica
Sean \(z\) y \(w\) dos complejos dados en su forma binómica:
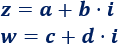
La suma de los complejos \(z\) y \(w\) es un número complejo cuya parte real es la suma de las partes reales y cuya parte imaginaria es la suma de las partes imaginarias:
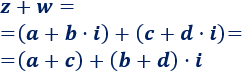
La resta es análoga, pero restando:
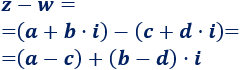
Problema 1
Sumar y restar los siguientes números complejos:
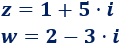
Solución:
Calculamos la suma \(z+w\):
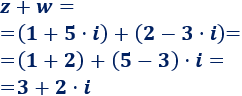
Calculamos la resta \(z-w\):
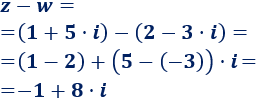
2. Multiplicar y dividir en forma binómica
Sean \(z\) y \(w\) dos complejos dados en su forma binómica:
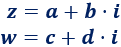
Producto:
La multiplicación de los complejos \(z\) y \(w\) se define como
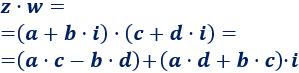
Nota: para obtener la fórmula, podéis calcular el producto como si fuera un producto de binomios, teniendo en cuenta que \(i^2=-1\).
Inverso:
El inverso multiplicativo del complejo \(w=c+di\) se define como
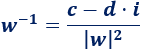
siendo \(|w|^2\) el cuadrado del módulo de \(w\):
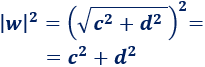
Cociente:
La división de los complejos \(z\) y \(w\) se define como
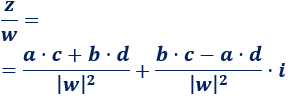
Nota: para obtener la fórmula, podéis calcular el producto de \(z\) por el inverso multiplicativo de \(w\).
Problema 2
Calcular el inverso multiplicativo de los siguientes complejos:
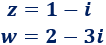
Solución:
Calculamos el módulo de \(z\) y el de \(w\):
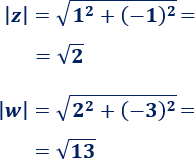
Calculamos el inverso de \(z\):
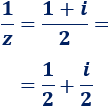
Calculamos el inverso de \(w\):
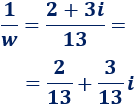
Problema 3
Multiplicar y dividir los complejos \(z\) y \(w\) y los complejos \(z\) y \(p\):
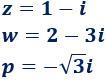
Solución:
Multiplicamos los complejos \(z\) y \(w\):
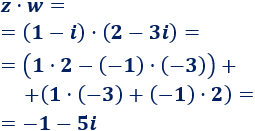
Dividimos los complejos \(z\) y \(w\):
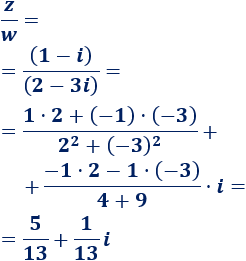
Multiplicamos los complejos \(z\) y \(p\):
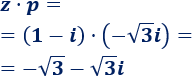
Dividimos los complejos \(z\) y \(p\):
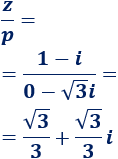
3. Multiplicar y dividir en forma polar
Sean los números complejos \(z\) y \(w\) dados en su forma polar:
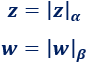
donde \(|z|\) y \(\alpha\) son el módulo y el argumento de \(z\) y \(|w|\) y \(\beta\) son los de \(w\).
Entonces,
-
Su producto es el complejo cuyo módulo es el producto de los módulos de los complejos y su argumento (ángulo) es la suma de sus argumentos
-
Su cociente es el complejo cuyo módulo es el cociente de los módulos de los complejos y su argumento es la resta de sus argumentos.
Dicho en fórmulas,
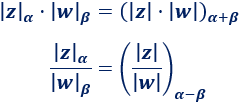
Si utilizamos la notación de Euler:
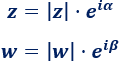
Entonces,
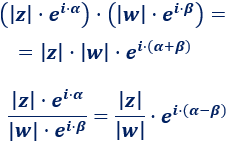
Problema 4
Multiplicar y dividir los complejos \(z\) y \(w\) y los complejos \(z\) y \(p\):
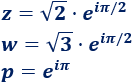
Solución:
Calculamos el producto \(z·w\):
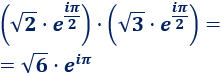
Calculamos el cociente \(z/w\):
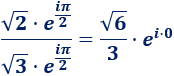
Calculamos el producto \(z·p\):
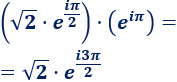
Calculamos el cociente \(z/p\):
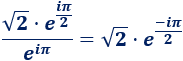
Más información y problemas resueltos de números complejos: