Introducción a los números complejos o imaginarios
En esta página vamos a ver qué son los números complejos o imaginarios y el porqué de su existencia en las matemáticas. A lo largo de la página, proponemos y resolvemos 4 problemas.
Índice de contenidos:
- El número \(i\)
- Definición de los números complejos
- Representación de los complejos
Otros temas de números complejos:
- Módulo y argumento de un complejo
- Operaciones entre números complejos
- Formas binómica, polar y trigonométrica
- Calculadora de operaciones entre complejos en forma binómica
1. El número \(i\)
Recordad que \(b\) es una raíz cuadrada del número \(a\) si su cuadrado es \(a\). Es decir, \(b=\sqrt{a}\) si \(b^2 = a\). Pero sabemos que cualquier número real al cuadrado es mayor o igual que \(0\), es decir,

Esto implica que la raíz cuadrada de un número negativo no existe. Por ejemplo, si \(b = \sqrt{-2}\), entonces \(b^2=-2\), pero hemos dicho que el cuadrado de un número real no puede ser negativo.
Sin embargo, cualquiera que haya trabajado con ecuaciones cuadráticas (o de segundo grado), sabe que encontrarse con raíces de números negativos es muy habitual. Por esta razón, los matemáticos inventaron números que no son reales y cuyo cuadrado puede ser un número negativo.
Se define la unidad imaginaria \(i\) como la raíz cuadrada del número real negativo \(-1\):
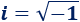
Ahora ya podemos calcular raíces cuadradas de números negativos.
Por ejemplo,
-
El número \(2·i\) es una raíz cuadrada de \(-4\) porque su cuadrado es \(-4\):
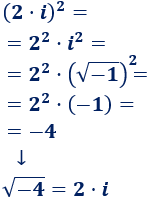
-
El número \(-2·i\) también es una raíz cuadrada de \(-4\) porque su cuadrado es \(-4\):
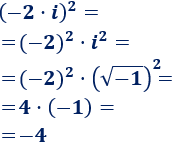
Problema 1
Calcular las raíces cuadradas de \(-25\), \(-16\) y \(-18\).
Solución:
Siguiendo el razonamiento de los ejemplos anteriores:
Las raíces cuadradas de \(-25\) son \(5i\) y \(-5i\):
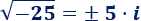
Las raíces cuadradas de \(-16\) son \(4i\) y \(-4i\):
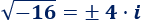
Las raíces cuadradas de \(-18\) son
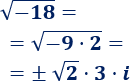
2. Definición de los números complejos
Ahora que ya sabemos qué es la unidad imaginaria (es decir, \(i\)), vamos a definir los números complejos (en su forma binómica).
Un número complejo, \(z\), es la suma de un número real \(a\) más un número real \(b\) multiplicado por la unidad imaginaria \(i\):

El número real \(a\) se llama parte real del complejo \(z\) y el número real \(b\) se llama parte imaginaria de \(z\).
El conjunto de todos los números se representa por \(\mathbb{C}\).
Nota: la suma \(a+b·i\) no la podemos simplificar, al igual que no podemos simplificar la expresión algebraica \(1+x\).
Problema 2
Determinar la parte real y la parte imaginaria de los siguientes números complejos:
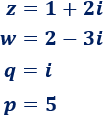
Solución:
El número complejo \(z=1+2i\) tiene parte real \(1\) y parte imaginaria \(2\).
El número complejo \(w=2-3i\) tiene parte real \(2\) y parte imaginaria \(-3\).
El número complejo \(q=i\) tiene parte real \(0\) y parte imaginaria \(1\).
El número real \(p=5\) es también un número complejo con parte real \(5\) y parte imaginaria \(0\).
Problema 3
Deducir la relación existente entre los números reales \(\mathbb{R}\) y los números complejos \(\mathbb{C}\).
Solución:
Los números reales son números complejos con parte imaginaria igual a \(0\). Si \(x\) es un número real, entonces es el número complejo \(z = x + 0i = x\).
Por tanto, los números reales están contenidos en los complejos:
$$ \mathbb{R} \subset \mathbb{C} $$
3. Representación de los números complejos
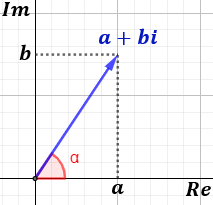
La forma habitual de representar a los números complejos es hacerlo como vectores del plano. Pero el plano se denomina, en este caso, plano complejo.
El complejo \(z=a+bi\) se representa como el vector con coordenadas \( (a,b) \):
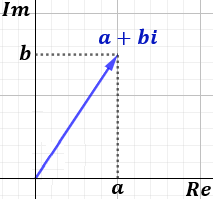
- El eje horizontal es el eje real.
- El eje vertical es el eje imaginario.
La longitud del vector se denomina módulo del complejo \(z\).
El ángulo que forma el vector con la parte positiva del eje real se denomina argumento del complejo \(z\):
Más información: módulo y argumento de un complejo.
Problema 4
Representar los siguientes números imaginarios:
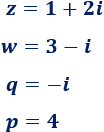
Solución:
Representación del complejo \(z=1+2i\):

Representación del complejo \(w=3-i\):
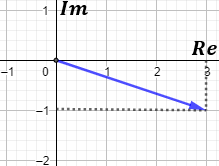
Representación del complejo \(q=-i\):
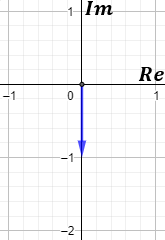
Representación del complejo \(p=4\):
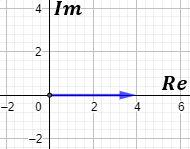
Las imágenes son provienen de la página números complejos en forma polar.
Más información y problemas resueltos de números complejos: