Módulo y argumento de los números complejos
En esta página vamos a definir el módulo, el argumento y el conjugado de un complejo y a enunciar sus propiedades básicas.
Índice de contenidos:
- Módulo y argumento
- Interpretación geométrica
- Conjugado
- Propiedades básicas
Otros temas de números complejos:
- Introducción a los números complejos
- Operaciones entre números complejos
- Formas binómica, polar y trigonométrica
- Calculadora de operaciones entre complejos en forma binómica
1. Módulo y argumento
Dado un número complejo en su forma binómica \(z = a+bi\),
Se define el módulo de \(z\) como
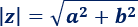
Se define el argumento de \(z\) como

Nota 1: la función arcotangente proporciona el ángulo entre -45º y 45º.
Nota 2: observad que, por ejemplo, la función arcotangente proporciona el mismo ángulo para \(z = a-bi\) y para \(w = -a+bi\). Sin embargo, \(z\) y \(w\) están en cuadrantes distintos, así que su argumento es distinto. Para solucionar esto:
-
Si el complejo está en el segundo cuadrante (\(a<0\), \(b>0\)), hay que sumar 180º al ángulo obtenido.
-
Si el complejo está en el tercer cuadrante (\(a<0\), \(b<0\)), hay que restar 180º al ángulo obtenido.
Nota 3: si \(a=0\), el argumento es
- 0° (0 radianes) si \(b=0\)
- 90° (\(\pi /2\) radianes) si \(b> 0\)
- 270° (\(3\pi /2\) radianes) si \(b< 0\)
Además, se denomina argumento principal de \(z\), \(Arg(z)\), al argumento de \(z\) en el intervalo \(\left]-180^\circ , 180^\circ \right]\) o, si es en radianes, \(\left]-\pi , \pi \right]\).
2. Interpretación geométrica
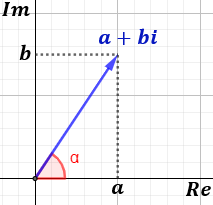
Si representamos el complejo \(z = a+bi\) en el plano complejo, su longitud es su módulo y el ángulo que forma con la parte positiva del eje horizontal es su argumento:
Problema 1
Calcular el módulo y el argumento de los siguientes números complejos:
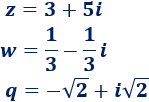
Solución:
Calculamos el módulo de \(z=3+5i\):
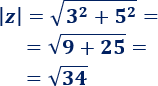
Calculamos el argumento de \(z\):
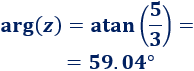
Calculamos el módulo de \(w=1/3-i/3\):
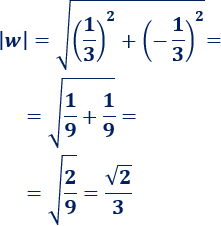
Calculamos el argumento de \(w\):
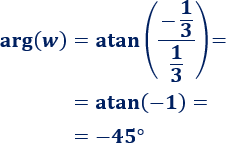
El ángulo de -45° es equivalente al ángulo de 270°.
Calculamos el módulo de \(q=-\sqrt{2}+i\sqrt{2}\):
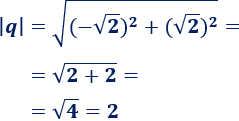
Calculamos el argumento de \(q\):
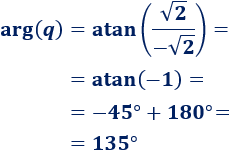
Hemos sumado 180º porque el complejo está en el segundo cuadrante.
3. Conjugado
Dado un número complejo en su forma binómica \(z = a+bi\), se define su conjugado como
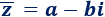
Interpretación geométrica
Si representamos un complejo y su conjugado, son simétricos respecto del eje horizontal:
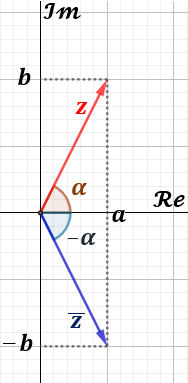
Tened en cuenta que la longitud de los vectores es la misma (tienen el mismo módulo) y los argumentos son iguales porque la arcotangente es una función impar:
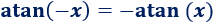
Problema 2
Calcular el complejo conjugado de los siguientes números complejos:
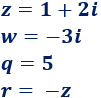
Solución:
Sólo tenemos que cambiar el signo de la parte imaginaria (si la hay):
El conjugado de \(z=1+2i\) es

El conjugado de \(w=-3i\) es
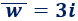
El conjugado de \(q=5\) es
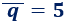
El conjugado de \(-z=-1-2i\) es
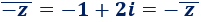
4. Propiedades
Omitimos las demostraciones de las propiedades porque son muy sencillas, pero podéis encontrarlas en propiedades de los complejos.
Propiedad 1
Conjugado del conjugado:

Propiedad 2
Conjugado de la suma:

Propiedad 3
Conjugado del producto de complejos:

Propiedad 4
Producto de un complejo por su conjugado:
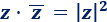
Propiedad 5
Conjugado del cociente de complejos:
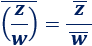
Propiedad 6
Suma de un complejo con su conjugado:
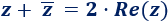
Propiedad 7
Resta de un complejo con su conjugado:

Propiedad 8
El módulo es no negativo:

Propiedad 9
Módulo del conjugado:
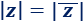
Propiedad 10
Módulo del producto de complejos:
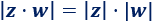
Propiedad 11
Módulo del inverso de un complejo:
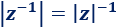
Propiedad 12
Módulo de la división de dos complejos:
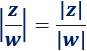
Propiedad 13
Módulo de la suma de complejos:

Más información y problemas resueltos de números complejos: