Formas binómica, trigonométrica y polar de los números complejos
En esta página vamos a ver las principales representaciones de los números complejos (binómica, trigonométrica y polar) y cómo pasar de una a otra. A lo largo de la página, proponemos y resolvemos 7 problemas.
Nota: escribiremos todos los ángulos en grados, pero también puede hacerse en radianes.
Índice de contenidos:
- Introducción
- Forma binómica
- Forma trigonométrica
- Forma polar
Otros temas de números complejos:
- Introducción a los números complejos
- Módulo y argumento de un complejo
- Operaciones entre números complejos
- Calculadora de operaciones entre complejos en forma binómica
1. Introducción
Normalmente, los complejos se definen en su forma binómica \(z=a+bi\), donde \(a\) y \(b\) son números reales llamados parte real y parte imaginaria, respectivamente, del complejo \(z\).
No obstante, existen otras formas de representar a un número complejo. Estas otras formas son la polar y la trigonométrica. En esta página vamos a ver las tres formas de representar complejos y cómo pasar de una a otra.
Por ejemplo, tres formas distintas de representar un mismo número complejo \(z\):
- \(z = 3\sqrt{2}·e^{i·135^\circ}\) (forma polar)
- \(z = -3+3i\) (forma binómica)
- \(z = 3\sqrt{2}·(cos(135^\circ )+i·sin(135^\circ )) \) (forma trigonométrica)
Cada una de las formas presenta sus ventajas y sus inconvenientes. Por ejemplo, multiplicar y dividir complejos es más rápido en forma polar, pero sumar y restar es más fácil en la forma binómica.
2. Forma binómica
Como ya hemos dicho, en la forma binómica, un complejo \(z\) se escribe como la suma de un número real \(a\) y un número real \(b\) multiplicado por la unidad imaginaria \(i\):

El número \(a\) es la parte real de \(z\) y \(b\) es la parte imaginaria de \(z\).
Problema 1
¿Cuál es la parte real y la imaginaria de los siguientes complejos?
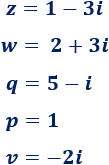
Solución:
El complejo \(z=1-3i\) tiene parte real 1 y parte imaginaria -3.
El complejo \(w= 2+3i\) tiene parte real 2 y parte imaginaria 3.
El complejo \(q=5-i\) tiene parte real 5 y parte imaginaria -1.
El número real \(p=1\) es también un número complejo con parte real 1 y parte imaginaria \(0\).
El complejo \(v=-2i\) tiene parte real \(0\) y parte imaginaria -2.
3. Forma trigonométrica
La forma trigonométrica del complejo \(z=a+bi\) es
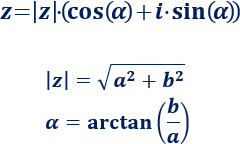
Importante
El ángulo que proporciona la función arcotangente es siempre entre -45° y 45°.
Si el complejo pertenece el primer cuadrante (\(a> 0\), \(b>0\)) o al cuarto (\(a> 0\), \(b<0\)), el ángulo obtenido es el argumento del complejo.
Sin embargo, si el complejo está en el segundo cuadrante (\(a<0\), \(b>0\)), hay que sumarle 180°. Y si está en el tercer cuadrante, (\(a<0\), \(b<0\)), hay que restarle 180°.
Hay una función proporciona directamente el argumento: \(atan2(a,b)\).
Veamos el significado de \(|z|\) y \(\alpha \) que aparecen en la forma trigonométrica (y en la polar). Recordad que el complejo \(z=a+bi\) se representa en el plano como el vector con coordenadas \((a,b)\):
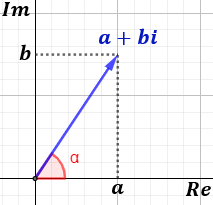
Las formas trigonométrica y polar se escriben con la longitud del vector (módulo del complejo) y el ángulo que forma con el eje horizontal positivo (argumento del complejo).
La longitud del vector se denomina módulo de \(z\), se representa como \(|z|\) y es la raíz cuadrada de la suma del cuadrado de la parte real y de la parte imaginaria:
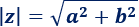
El ángulo que forma el vector con la parte positiva del eje horizontal se denomina argumento de \(z\) y, aplicando un poco de trigonometría, se calcula con la inversa de la tangente:
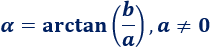
Si la parte real es \(a=0\), el argumento de \(z=a+bi\) es
-
0° si \(b=0\).
-
90° si \(b> 0\).
-
270° si \(b< 0\).
Notas:
- El argumento puede darse en grados o radianes.
- Se denomina argumento principal al argumento si se proporciona en el intervalo \(\left( -180^\circ , 180^\circ \right]\) (en radianes, \(\left( -\pi , \pi \right]\)).
Problema 2
Escribir los siguientes complejos en forma trigonométrica:
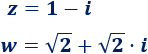
Solución:
Calculamos el módulo de \(z=1-i\):
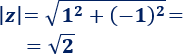
Calculamos el ángulo que forma \(z\) (argumento):

Por tanto, la forma trigonométrica de \(z\) es
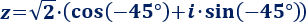
Calculamos el módulo de \(w=\sqrt{2}+\sqrt{2}·i\):
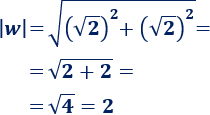
Calculamos ahora el argumento de \(w\):

Por tanto, la forma trigonométrica de \(w\) es
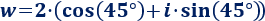
Problema 3
Representar y escribir en forma trigonométrica los complejos \(z=-i\) y \(w=2\).
Solución:
Podemos escribir el complejo \(z=-i\) como

Calculamos el módulo de \(z\):
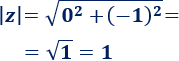
Si representamos el complejo, como la parte real es 0, el vector está sobre el eje vertical. Como la parte imaginaria es negativa, el vector está en la parte negativa del eje:
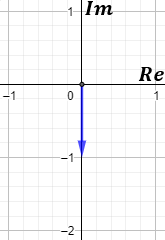
El ángulo que forma el vector es 270° ó -90°.
Por tanto, la forma trigonométrica de \(z=-i\) es
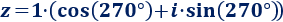
Podemos escribir el complejo \(w=4\) como

Calculamos el módulo de \(w\):
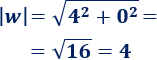
Calculamos el argumento de \(w\):

Por tanto, la forma trigonométrica de \(w=4\) es
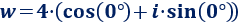
Su representación es
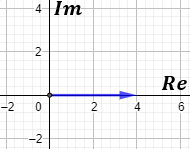
Cuando tenemos un complejo escrito en forma trigonométrica, ya lo tenemos casi en forma binómica. Falta calcular el seno y el coseno del argumento y multiplicar por el módulo.
Problema 4
Escribir los siguientes complejos en forma binómica:
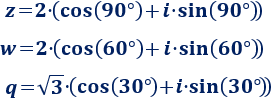
Solución:
El coseno de 90° es 0 y el seno de 90° es 1. Por tanto, la forma binómica de \(z\) es
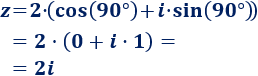
El coseno de 60° es \(1/2\) y el seno de 60° es \(\sqrt{3}/2\). Por tanto, la forma binómica de \(w\) es
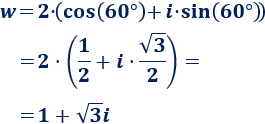
El coseno de 30° es \(\sqrt{3}/2\) y el seno de 30° es \(1/2\). Por tanto, la forma binómica de \(q\) es
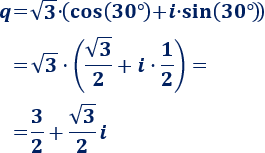
4. Forma polar
En la forma polar, el complejo se escribe en función de su módulo \(|z|\) y su argumento \(\alpha \) como

También, como

E, incluso, como
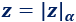
Por ejemplo, el complejo \(z=1+i\) en forma polar es
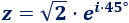
La forma polar es útil a la hora de multiplicar y dividir complejos y también para visualizarlos en el plano complejo.
El cambio de la forma polar a la forma trigonométrica se realiza utilizando la siguiente identidad (llamada fórmula de Euler):
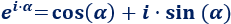
Problema 5
Escribir los siguientes complejos en forma polar:
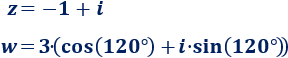
Solución:
Calculamos el módulo del complejo \(z\):
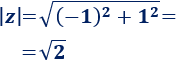
Calculamos su argumento:

Nota: hemos sumado 180º grados al ángulo obtenido (-45º) porque el complejo está en el segundo cuadrante).
Por tanto, la forma polar de \(z\) es

La forma polar de \(w\) es directa:

Problema 6
Escribir los siguientes complejos en forma trigonométrica:
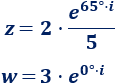
Solución:
Como el módulo de \(z\) es \(2/5\) y su argumento es 65°,
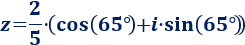
Como el módulo de \(w\) es 3 y su argumento es 0°,
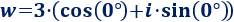
Problema 7
Escribir los siguientes complejos en forma binómica:
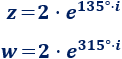
Solución:
Para pasar a la forma binómica tenemos que pasar por la trigonométrica.
Escribimos \(z\) en forma binómica:
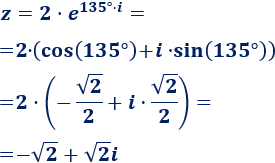
Escribimos \(w\) en forma binómica:
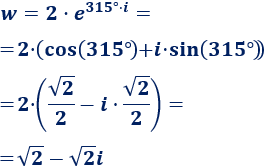
Más información y problemas resueltos de números complejos: