Calculadora para resolver sistemas de ecuaciones 2x2
Recordad que un sistema de ecuaciones lineales puede tener una única solución, infinitas soluciones o ninguna solución.
La calculadora sólo proporciona la solución si el sistema tiene una única solución.
Para resolver un sistema, podemos aplicar los siguientes métodos:
- Métodos básicos: sustitución, reducción e igualación.
- Método gráfico
- Regla de Cramer (matrices)
- Eliminación de Gauss (matrices)
Enlace recomendado: problemas resueltos de sistemas de ecuaciones.
Calculadora
La calculadora admite números enteros y decimales. Para fracciones, podéis usar la calculadora de sistemas.
|
||||
| \(·x +\) | \(·y = \) | |||
| \(·x +\) | \(·y = \) |
Ejemplo: método de sustitución
Vamos a resolver el sistema
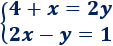
1. Aislamos una incógnita
Vamos a aislar la x de la primera ecuación. Como su coeficiente es 1, sólo tenemos que pasar el 4 restando al otro lado:
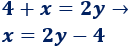
Ya tenemos aislada la incógnita x.
2. Sustituimos la incógnita en la otra ecuación
Como tenemos que la incógnita x es igual 2y-4, escribimos 2y-4 en lugar de la x en la segunda ecuación (sustituimos la x):
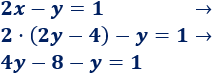
Observad que hemos utilizado paréntesis porque el coeficiente 2 tiene que multiplicar a todos los términos.
3. Resolvemos la ecuación obtenida:
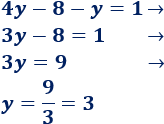
Ya sabemos una incógnita: y=3.
4. Calculamos la otra incógnita sustituyendo:
Al despejar la incógnita x teníamos

Como conocemos y=3, sustituimos en la ecuación:
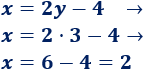
Por tanto, la otra incógnita es x=2.
La solución del sistema es
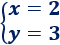
Más ejemplos en métodos para resolver sistemas.