Integración por sustitución o cambio de variable
En esta página explicamos el método de integración por sustitución o cambio de variable a través de 4 ejemplos.
Como es de suponer por su nombre, el método de sustitución consiste en aplicar un cambio de variable para transformar el integrando en una función más simple de integrar.
Notación: escribiremos la función logaritmo natural (logaritmo en base \(e\)) como \(ln(·)\).
El método
Explicaremos el método mediante ejemplos, pero el esquema es el siguiente (si resulta demasiado técnico, podéis dejarlo pasar).
Dada la integral indefinida
$$\int{ f(x) dx }$$
1. Definimos un cambio de variable \(s = h(x)\).
2. Calculamos la inversa del cambio de variable, es decir, \( x = h^{-1}(s)\), y la derivamos:
$$ dx = \frac{1}{h'(s)} ds $$
3. Aplicamos el cambio en la integral:
$$ \int{ f(x) dx } = $$
$$ = \int{ f(h^{-1}(s))\cdot \frac{1}{h'(s)} ds }$$
4. Resolvemos la integral obtenida.
5. Para terminar, deshacemos el cambio de variable (escribimos la primitiva en función de \(x\) en lugar de \(s\)).
Como se observa en los ejemplos que veremos, la elección del cambio de variable es la clave para que el método funcione. En la siguiente tabla se recogen los cambios que habitualmente suelen funcionar:
Tabla con cambios útiles

Integrales resueltas
Nota previa: algunas de las integrales que resolvemos son directas o se pueden resolver mediante otros métodos.
Integral 1
Integral con raíz cuadrada.
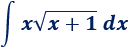
Solución:
Aplicaremos el cambio de variable
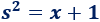
Escogemos este cambio porque así, al sustituir en la integral, la raíz cuadrada desaparece.
Calculamos la inversa del cambio de variable y derivamos:
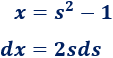
Sustituimos en la integral (cambiamos \(x\) por \(s^2-1\) y \(dx\) por \(2sds\)):
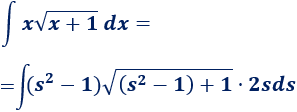
Operamos en el integrando para simplificarlo:
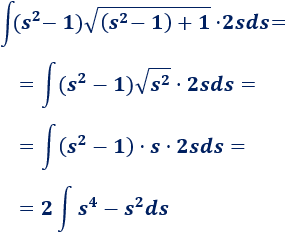
Resolvemos la integral:
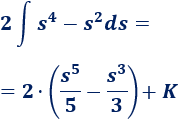
Simplificamos un poco el resultado:
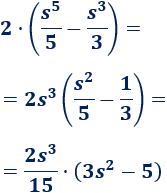
Deshacemos el cambio de variable:
Como \(s = \sqrt{x+1}\),
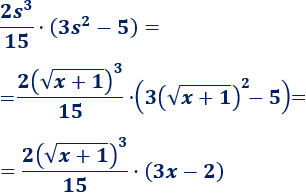
Por tanto,
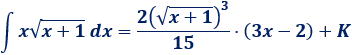
Nota final: normalmente, para eliminar una raíz cuadrada elegimos el cambio \(s =\) (radicando)\(^2\).
Integral 2
Integral con exponenciales.
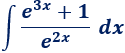
Solución:
Como se indica en la tabla, cuando tenemos exponenciales aplicamos el cambio \(s = e^x\).
Despejamos \(x\) y derivamos:
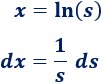
Aplicamos el cambio de variable (escribiendo directamente \(s\) en lugar de \(e^x\) y \(1/s ds\) en lugar de \(dx\)):
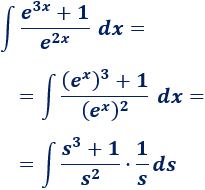
Simplificamos y resolvemos la integral:
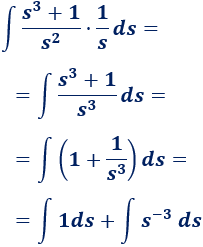
Las dos integrales que tenemos son, más o menos, directas:
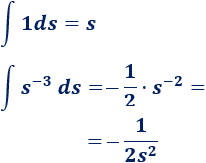
Por tanto, tenemos
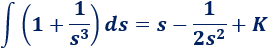
Deshacemos el cambio de variable:
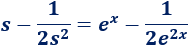
Con lo que la integral inicial es
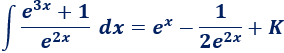
Integral 3
Integral con funciones trigonométricas.
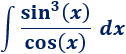
Solución:
Tanto el exponente del seno como el del coseno son impares, así que, según la tabla, podemos aplicar el cambio \( s = cos(x)\) o el cambio \( s = sin(x)\).
Nos decidimos por el primero: \( s = cos(x)\).
Despejamos \(x\) y derivamos:
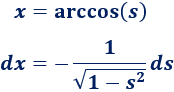
Calculamos el cubo del seno en la nueva variable:
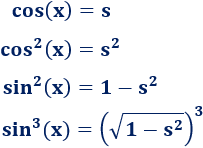
Aplicamos el cambio de variable:
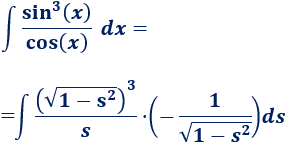
Simplificamos (las raíces van a desaparecer):
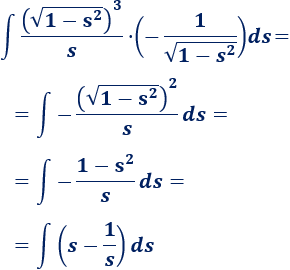
Calculamos la integral obtenida:
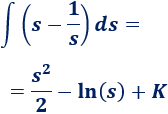
Deshacemos el cambio de variable:
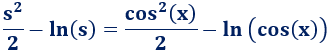
Por tanto,
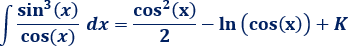
Para simplificar el resultado de la siguiente integral, utilizaremos
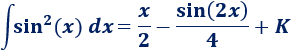
Integral 4
Integral con la raíz \( \sqrt{a^2-b^2x^2}\).
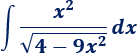
Nota: la resolución de la integral es sencilla, pero bastante larga.
Solución:
Teniendo en cuenta la tabla, aplicamos el cambio
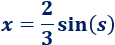
Nota: en los otros casos, la tabla nos proporciona la nueva variable \(s\) en función de \(x\). En este caso, es la inversa.
Derivamos:
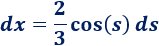
Calculamos \(s\):
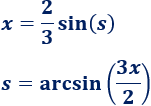
Sustituimos en la integral:
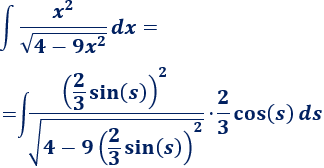
Simplificamos el integrando y resolvemos la integral:
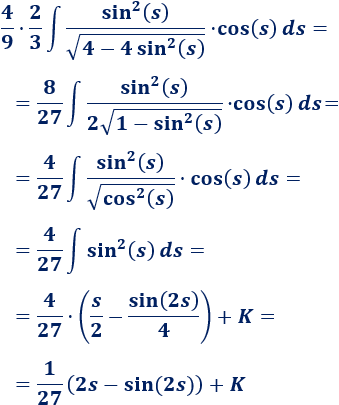
Finalmente, deshacemos el cambio de variable:
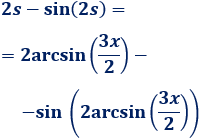
Por tanto,

Nota: utilizando fórmulas, el resultado puede simplicarse bastante, pero omitimos este cálculo por su irrelevancia en el método de integración.
Más integrales por sustitución: 10 integrales resueltas por cambio de variable.