Integrales directas o inmediatas
Las integrales directas o inmediatas son las integrales que por su sencillez no requieren la aplicación de un método de integración para su resolución.
Para resolver estas integrales necesitamos conocer las derivadas de las funciones elementales (tabla de derivadas (PDF)), la regla de la cadena y las propiedades de las integrales (las veremos más adelante).
En esta página vamos a resolver 10 integrales directas, pero antes vamos a recordar los conceptos y las propiedades que necesitamos.
Notación: escribiremos la función logaritmo natural (logaritmo en base \(e\)) como \(ln(·)\).
1. ¿Qué es la integral indefinida?
Recordamos al lector que el resultado de la integral indefinida de la función \(f(x)\) es cualquier función \(F(x)\) cuya derivada sea \(f(x)\). Es decir,
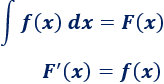
La función \(F(x)\) se llama primitiva o antiderivada de \(f(x)\).
Obviamente, la integración y la derivación son operaciones inversas (aunque históricamente fueron estudiadas por separado).
2. ¿Qué es la constante de integración?
El resultado de todas las integrales indefinidas debe contener la llamada constante de integración, normalmente escrita como \(K\) o \(C\).
Veamos un ejemplo muy explicativo:
La derivada de la función \(F(x) = x^2\) es \(F'(x) = 2x\). Esto significa, por tanto, que \(F\) es la integral de \(f(x) = 2x\).
Sin embargo, como la derivada de una constante es 0, las siguientes funciones también son primitivas de \(f(x) = 2x\):
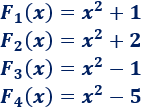
Queda claro que la función tiene infinitas primitivas.
En el ejemplo vemos que la diferencia entre las primitivas es una constante. Esta constante se representa en las integrales mediante la constante de integración \(K\):
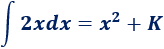
3. ¿Qué es \(dx\)?
En una integral es imprescindible indicar cuál es la variable de integración, es decir, la variable de la función que se integra.
En el integrando (función que deseamos integrar) pueden aparecer varias letras (variables, parámetros, constantes, etc.), por lo que siempre es necesario indicar la variable de integración, esto es, la variable de la función a integrar.
Veamos algunos ejemplos:
La integral de \(2xy\) respecto de \(x\) es
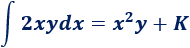
La integral de \(2xy\) respecto de \(y\) es
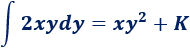
La integral de \(2xy^2\) respecto de \(y\) es
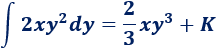
La integral de \(2xy^2\) respecto de \(x\) es
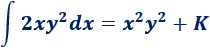
Queda claro que no es lo mismo integrar respecto de una variable que de otra.
Además de esto, el símbolo \(dx\) no es un factor del integrando y, por tanto, es incorrecto tratarlo como tal. Hay que evitar escribir expresiones como

4. Propiedades de las integrales
Las propiedades básicas de las integrales son imprescindibles para el cálculo integral y son muy sencillas:
-
Integral de una función por una constante:
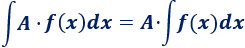
-
Integral de una suma de funciones:
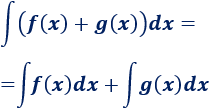
Integrales directas resueltas
Vamos a empezar por integrales muy sencillas. Con la práctica, muchos de los pasos que seguimos los haréis de cabeza.
Consejo: comprobad el resultado (sólo tenéis que derivarlo): si la derivada del resultado es el integrando, la integral es correcta.
Integral 1
Integral de una constante:
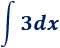
Solución:
La derivada de \(3x\) es \(3\), así que
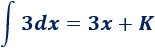
Integral 2
Integral de un monomio:
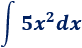
Solución:
Extraemos la constante:
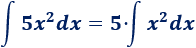
La derivada de \(x^3\) es \(3x^2\). Si conseguimos un \(3\) en el integrando, entonces tendríamos la derivada de \(x^3\) en el integrando. Esto se consigue multiplicando y dividiendo por \(3\):
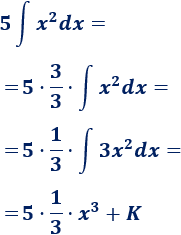
Por tanto,
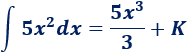
Nota: del razonamiento anterior se deduce la fórmula para \(n\neq -1 \)
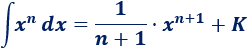
Integral 3
Integral de un polinomio:
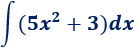
Solución:
Como el integrando es un polinomio, su primitiva también lo es (con un grado más).
Podemos escribir la integral como una suma de integrales:
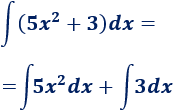
Ya sabemos cómo resolver estas dos integrales:
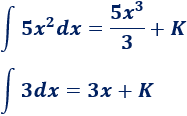
Por tanto,
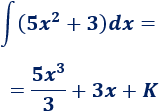
Integral 4
Integral de un cociente de polinomios:
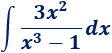
Solución:
Siempre que tengamos un cociente en el integrando, tenemos que comprobar si el numerador es la derivada del denominador.
Esto es lo que ocurre en esta integral porque la derivada de \(x^3-1\) es \(3x^2\). Por tanto, la integral tiene la forma
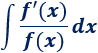
Estas integrales son muy fáciles de resolver porque son un logaritmo.
Derivamos el logaritmo de una función:
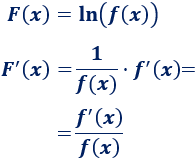
Por tanto, tenemos la fórmula
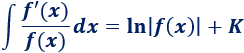
Nota: escribiremos el argumento del logaritmo en valor absoluto ya que éste nunca puede ser negativo.
Calculamos la integral:
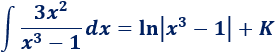
Integral 5
Integral de una función trigonométrica:
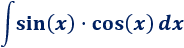
Solución:
Cuando tenemos un producto, tenemos que comprobar si es el producto de una función por su derivada. Es lo que ocurre en esta integral.
Calculamos, por la regla de la cadena, la derivada del cuadrado de una función:
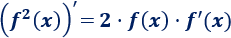
Por tanto, tenemos la fórmula
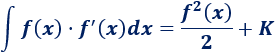
Luego nuestra integral es
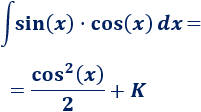
Integral 6
Integral de una raíz cúbica:
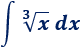
Solución:
Cuando tenemos raíces, intentaremos simplificar el integrando escribiéndolas como potencias:
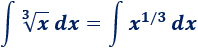
La derivada de \(x^n\) es \(n·x^{n-1}\).
La constante que multiplica no supone un problema.
Buscamos una función \(x^n\) cuya derivada sea \(x^{1/3}\):
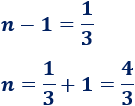
Calculamos la derivada de \(x^{4/3}\):
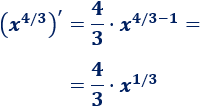
Por tanto, sólo necesitamos escribir \(4/3\) en el integrando para que sea la derivada de \(x^{4/3}\):
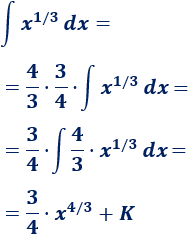
Nota: del razonamiento anterior se deduce la fórmula
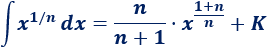
Integral 7
Integral de un polinomio por una raíz cuadrada:
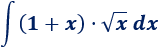
Solución:
Tenemos un producto en el integrando, pero ninguno de los factores es la derivada del otro. Así que, la primitiva no es el cuadrado de ninguno de los factores.
Escribimos la raíz como una potencia y descomponemos la integral en una suma:
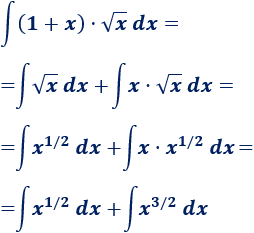
Estas integrales son parecidas a la calculada anteriormente.
La primera es
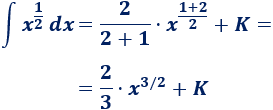
La segunda es
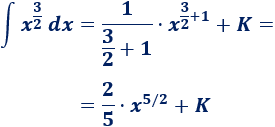
Por tanto,
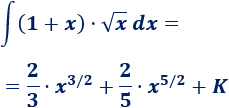
Integral 8
Integral de un cociente (logaritmo entre monomio):
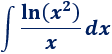
Solución:
Esta integral parece complicada a primera vista: se trata de un cociente, pero el numerador no es la derivada del denominador.
Comprobamos si es la derivada del cuadrado del numerador:
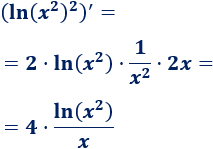
En efecto, lo es. Por tanto,
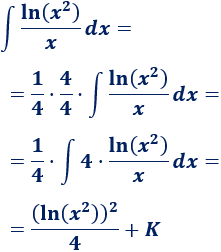
Integral 9
Integral del cuadrado del coseno:
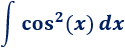
Solución:
Hemos tardado en proponer esta integral porque es sencilla (y típica) si conocemos la identidad trigonométrica siguiente:
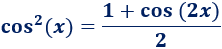
Por tanto,
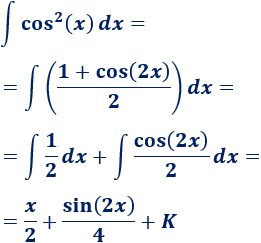
Integral 10
Integral de un cociente con raíz en el denominador:
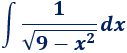
Solución:
Esta integral también es típica y fácil, aunque el procedimiento hay que verlo alguna vez para saber aplicarlo. Sólo tenemos que operar para conseguir un arcoseno.
Recordad que la derivada del arcoseno es
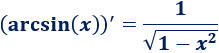
El integrando es casi la derivada del arcoseno.
Operamos:
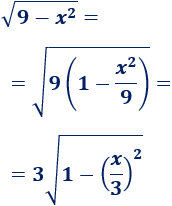
Por tanto,
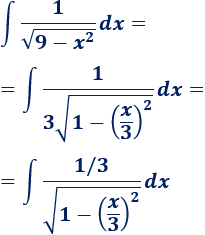
Y ya hemos terminado porque
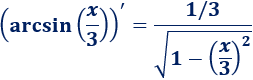
Así que
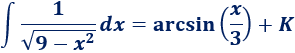
Más integrales directas o inmediatas resueltas.