Árbol de Pitágoras (fractal)
El árbol de Pitágoras es un fractal plano propuesto en 1942 por el profesor de matemáticas Albert E. Bosman. El nombre del fractal se debe a que cada trío de cuadrados en contacto es la típica figura que se utiliza para demostrar geométricamente el teorema de Pitágoras.
En esta página vamos a ver cómo se construye este fractal y algunas de sus propiedades. También, modificamos la construcción del fractal para generar otros fractales similares (variantes del árbol).
Índice:
- Construcción
- Propiedades
- Variantes
- Referencias
Construcción
El árbol de Pitágoras es el límite de una construcción iterativa que comienza con un cuadrado al que se le van añadiendo cuadrados cada vez más pequeños[3]:
-
El paso inicial (\(n=0\)) es un cuadrado de lado \(L\) (por comodidad, suponemos \(L=1\)):

-
En la primera iteración, se añaden dos cuadrados de lado \(L·\sqrt{2}/2\) en las esquinas superiores del cuadrado como se muestra en la siguiente figura (formado ángulos de 45°):

-
En las siguientes iteraciones, se repite el paso anterior en cada unos de los nuevos cuadrados añadidos en el paso anterior:

Tabla con las primeras iteraciones:

|

|

|
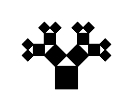
|
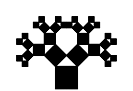
|
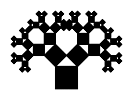
|
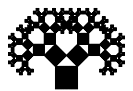
|

|

|

|
Por cada cuadrado añadido en una iteración, se añaden otros dos cuadrados en la siguiente, por lo que el número de cuadrados nuevos en la iteración \(n\) es \(2^n\) y el número total de cuadrados es
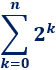
Propiedades
En [1] se demuestra que el límite de la construcción anterior (\(n\to \infty\)) existe y es el fractal autosemejante llamado árbol de Pitágoras. Hay que decir, sin embargo, que el fractal (el límite) depende del conjunto inicial.
El árbol está formado por dos copias de sí mismo con factor de contracción de \(\sqrt{2}/2\), así que su dimensión de Hausdorff es 2[2]:
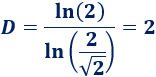
Tomando como conjunto inicial al cuadrado de lado unidad, la construcción anterior es la descrita por el sistema de funciones iteradas (IFS) formado por[2]
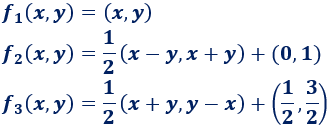
Si eliminamos la función \(f_1\) del IFS anterior, entonces el fractal resultante está formado por las hojas terminales del árbol. Este fractal es muy parecido al dragón o curva C de Lévy, también de dimensión 2:
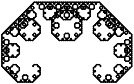
\(n=11\)
Además, el árbol de Pitágoras (con \(L=1\)) cabe dentro de un rectángulo de base 6 y altura 4:
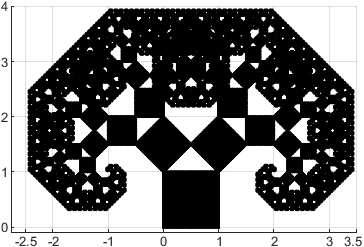
A continuación, demostramos la propiedad anterior:
Para calcular la altura, representamos el cuadrado de la izquierda en las iteraciones impares y el derecho en las pares. Así, obtenemos la siguiente sucesión de cuadrados:

La altura del conjunto inicial es 1.
En el paso \(n=1\), hay que sumar \(\sqrt{2}·\sqrt{2}/2\) a la altura, que es lo que mide la diagonal del nuevo cuadrado.
En el paso \(n=2\), hay que sumar a la altura del nuevo cuadrado, que es \((\sqrt{2}/2)^2\).
Y, así, sucesivamente para todo \(n\). Por tanto, la altura del conjunto en el paso \(n\) (par) es
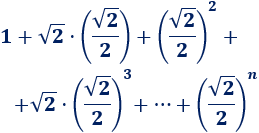
Por consiguiente, la altura del árbol de Pitágoras es la suma de las dos siguientes sucesiones (\(N\to \infty\)):
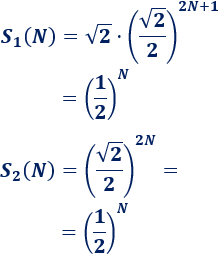
Son dos sucesiones geométricas con razón \(1/2\) y cuyos términos suman 2 (para \(N\to\infty\)):
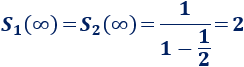
Luego la altura del árbol de Pitágoras es 4.
Para calcular la anchura, procedemos de una forma similar a la seguida anteriormente:

De nuevo, hay que sumar el lado del cuadrado en una iteración y la diagonal del cuadrado en la siguiente iteración. Por tanto, por lo anterior, sin sumar el cuadrado inicial, cada rama mide 3. Luego la anchura que ocupa el árbol de Pitágoras es 6.
Finalmente, del área \(A\) del árbol de Pitágoras sólo podemos decir que está entre 5 y 18, puesto que a partir de la quinta iteración aparecen auto-intersecciones.
Variantes
En el árbol de Pitágoras, el ángulo \(\alpha\) que forman los lados de los cuadrados que se añaden en cada iteración es de 45°. Si cambiamos el ángulo y, por tanto, el tamaño de los cuadrados, obtenemos otros árboles.
Por ejemplo, si el ángulo que forma el cuadrado de la izquierda es \(\alpha=60^\circ\) y el de la derecha es \(90^\circ - \alpha=30^\circ\), tenemos el siguiente árbol (9 iteraciones):
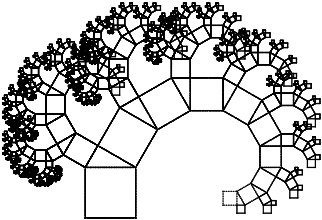
Nota: hemos utilizado el borde de un cuadrado unidad como conjunto inicial para que se aprecie mejor la estructura.
Aplicando trigonometría básica, para los ángulos \(\alpha \) y \(90^\circ - \alpha \), la razón de reducción de los lados de los cuadrados debe ser \(cos(\alpha)\) y \(sin(\alpha)\).
Referencias:
[1] Larry Riddle. Hausdorff convergence for Pythagorean tree.
[2] José L. Llopis. Fractales autosemejantes.
[3] Bosman, Albert E. De digitale vraagbaak voor het wiskundeonderwijs.